题目内容
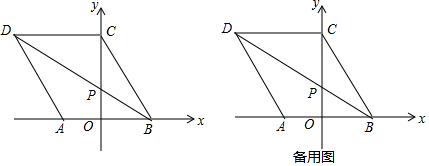
14.如图,在平面直角坐标系中,点B(3,0),点C(0,4),四边形ABCD是菱形,对角线BD于y轴交于点P.(1)请直接写出A点与D点坐标;
(2)动点M从B点出发以每秒1个单位的速度沿折线段B-A-D运动,设△AMP的面积为S(S≠0),运动时间为t(秒),求面积S与时间t之间的函数关系式,并直接写出自变量的取值范围;
(3)在(2)的条件下,是否存在一点M,使△DMP沿其一边翻折构成的四边形是菱形?若存在,求出点M的坐标;若不存在,请说明理由.
分析 (1)先求出BC,再利用菱形的性质即可得出AB=CD=5,即可得出点A,D坐标;
(2)先判断出△BOP≌△BKP,进而求出BK=3,CK=2,再利用勾股定理求出PK,PC,即可得出PO,同理求出PA=PC,最后分两种情况利用三角形的面积公式即可;
(3)分点M在AB上和AD上,利用勾股定理即可求出结论.
解答 解:(1)∵点B(3,0),点C(0,4),
∴BC=5,
∵四边形ABCD是菱形,
∴CD=AB=BC=5,CD∥AB,
∴A(-2,0),D(-5,4),
(2)如图1, 过点P作PK⊥BC于K,
过点P作PK⊥BC于K,
∵四边形ABCD是菱形,
∴∠CBD=∠ABD,
∵PO⊥AB,
∴PK=PO,
∴△BOP≌△BKP,
∴BK=OB=3,
∴CK=2,
在Rt△PKC中,CK2+PK2=PC2,
∴4+PK2=(5-PK)2,
∴PK=$\frac{3}{2}$,PC=$\frac{5}{2}$,
∴PO=$\frac{3}{2}$,
同理:连接PA,易证△DCP≌△DAP,
∴∠DCP=∠DAP=90°,PA=PC=$\frac{5}{2}$,
①S=$\frac{1}{2}$×$\frac{3}{2}$(5-t)=-$\frac{3}{4}$t+$\frac{15}{4}$(0≤t<5),
②S=$\frac{1}{2}$×$\frac{3}{2}$(t-5)=$\frac{3}{4}$t-$\frac{15}{4}$(5<t≤1-);
(3)①如图2, 当点M在AB上,DP=DM时,沿PM翻折,可得四边形为菱形,
当点M在AB上,DP=DM时,沿PM翻折,可得四边形为菱形,
在Rt△OPB中,BP=$\sqrt{O{P}^{2}+O{B}^{2}}$=$\frac{3\sqrt{5}}{2}$
过点D作DR⊥AB于R,DR=4,BR=8,
在Rt△DRB中,根据勾股定理得,DB=4$\sqrt{5}$,
∴DM=DP=$\frac{5\sqrt{5}}{2}$,
在Rt△DRM中,根据勾股定理得,RM=$\frac{\sqrt{61}}{2}$,
∴OM=5-$\frac{\sqrt{61}}{2}$,
∴M($\frac{\sqrt{61}}{2}$-5,0);
②如图3, 当点M在AD上,MD=MP时,沿DP翻折,可得四边形是菱形,
当点M在AD上,MD=MP时,沿DP翻折,可得四边形是菱形,
∴∠MDP=∠MPD,
∵∠MDP=∠CDP,
∴∠MPD=∠CDP,
∴PM∥CD,
过点M作MN⊥AB于N,
∴四边形MNOP是矩形,
∴MN=OP=$\frac{3}{2}$,MP=MD=ON=AN+2,
∴AM=5-DM=3-AN,
在Rt△AMN中,AN2+MN2=AM2,
∴AN=$\frac{9}{8}$,ON=$\frac{25}{8}$,
∴M(-$\frac{25}{8}$,$\frac{3}{2}$).
点评 此题是四边形综合题,主要考查了菱形的性质,矩形的判定和性质,折叠的性质,全等三角形的判定和性质,勾股定理,解(1)的关键是求出BC,解(2)的关键是利用勾股定理求出PK,PC,解(3)的关键是画出图形,是一道难度比较大的中考常考题.

| A. | 3x-2y | B. | 9x-6y | C. | 3x-2 | D. | 6x-4y |
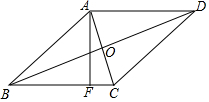 如图,在菱形ABCD中,对角线AC、BD交于点O,AF⊥BC于点F,若AC=2,BD=6,则AF=$\frac{3\sqrt{10}}{5}$.
如图,在菱形ABCD中,对角线AC、BD交于点O,AF⊥BC于点F,若AC=2,BD=6,则AF=$\frac{3\sqrt{10}}{5}$.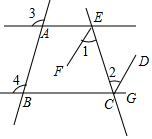 已知:如图,直线AE,BC被直线AB,EC所截,已知∠3=∠4,EF平分∠AEC,CD平分∠ECG,将下列证明EF∥CD的过程及理由填写完整.
已知:如图,直线AE,BC被直线AB,EC所截,已知∠3=∠4,EF平分∠AEC,CD平分∠ECG,将下列证明EF∥CD的过程及理由填写完整.