题目内容
9.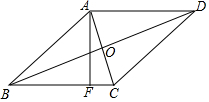 如图,在菱形ABCD中,对角线AC、BD交于点O,AF⊥BC于点F,若AC=2,BD=6,则AF=$\frac{3\sqrt{10}}{5}$.
如图,在菱形ABCD中,对角线AC、BD交于点O,AF⊥BC于点F,若AC=2,BD=6,则AF=$\frac{3\sqrt{10}}{5}$.
分析 由在菱形ABCD中,对角线AC、BD相交于点O,AC=2,BD=6,可求得菱形的面积与边长,继而求得答案.
解答 解:∵在菱形ABCD中,AC=2,BD=6,
∴OB=$\frac{1}{2}$BD=3,OA=$\frac{1}{2}$AC=1,AC⊥BD,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{10}$,
∵S菱形ABCD=$\frac{1}{2}$AC•BD=AB•AF,
∴AF=$\frac{1}{2}$×$\frac{AC•BD}{AB}$=$\frac{3\sqrt{10}}{5}$,
故答案为$\frac{3\sqrt{10}}{5}$.
点评 此题考查了菱形的性质以及勾股定理.注意菱形的面积等于对角线积的一半或底乘以高.

练习册系列答案
相关题目
4.下列各式中计算正确的是( )
| A. | $\sqrt{(-4)(-16)}$=$\sqrt{-4}$$•\sqrt{-16}$=(-2)(-4)=8 | B. | $\sqrt{8{a}^{2}}$=4a(a≥0) | ||
| C. | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{41+40}$$•\sqrt{41-40}$=9×1=9 | D. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 |
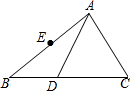 如图,△ABC中,D为BC边上的点,∠CAD=∠CDA,E为AB边的中点.
如图,△ABC中,D为BC边上的点,∠CAD=∠CDA,E为AB边的中点.

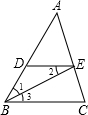 如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程.
如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程.