题目内容
5.用适当的方法解方程组:(1)$\left\{\begin{array}{l}{x+y=3}\\{2x+3y=8}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{4x-3y=1}\\{3x+2y=5}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+y=3①}\\{2x+3y=8②}\end{array}\right.$,
由①得y=3-x③,
把③代入②得2x+3(3-x)=8,
x=1,
把x=1代入③得,y=2
∴原方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$
(2)$\left\{\begin{array}{l}{4x-3y=1①}\\{3x+2y=5②}\end{array}\right.$,
由①×2得8x-6y=3③,
②×3得9x+6y=15④,
③+④得 x=1,
把x=1代入①得y=1,
∴原方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
15.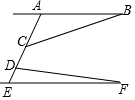 如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )
如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )
 如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )
如图,AB∥EF,∠BCD=135°,∠FDC=85°,则∠B+∠F的度数为( )| A. | 38° | B. | 40° | C. | 55° | D. | 60° |
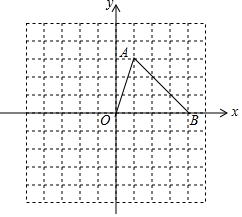 如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(1,3),B(4,0),O(0,0).
如图,在平面直角坐标系中,△ABO的三个顶点坐标分别为A(1,3),B(4,0),O(0,0).