题目内容

19．关于x的方程：x+$\frac{1}{x}$=c+$\frac{1}{c}$的解是x1=c，x2=$\frac{1}{c}$；x-$\frac{1}{x}$=c-$\frac{1}{c}$的解是x1=c，x2=-$\frac{1}{c}$，则x+$\frac{1}{x-3}$=c+$\frac{1}{c-3}$的解是x1=c，x2=3+$\frac{1}{c-3}$．

分析 根据方程根的定义得出答案即可．

解答 解：∵x+$\frac{1}{x}$=c+$\frac{1}{c}$的解是x1=c，x2=$\frac{1}{c}$；x-$\frac{1}{x}$=c-$\frac{1}{c}$的解是x1=c，x2=-$\frac{1}{c}$，
∴x+$\frac{1}{x-3}$=c+$\frac{1}{c-3}$可化为x-3+$\frac{1}{x-3}$=c-3+$\frac{1}{c-3}$，
x+$\frac{1}{x-3}$=c+$\frac{1}{c-3}$的解是x1=c，x2=3+$\frac{1}{c-3}$，
故答案为3+$\frac{1}{c-3}$．

点评 本题考查了分式方程的解，掌握分式方程的解的定义是解题的关键．

练习册系列答案
相关题目
9．（1）$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
（2）先化简再求值：$\frac{2x-1}{{x}^{2}-2x+1}$•（x-1），其中x=$\sqrt{2}$+1．
10．在整式乘法的学习中，我们采用了构造几何图形的方法研究代数式的变形问题，借助直观、形象的几何图形，加深对整式乘法的认识和理解，感悟代数与几何的内在联系．
现有边长分别为a，b的正方形Ⅰ号和Ⅱ号，以及长为a，宽为b的长方形Ⅲ号卡片足够多，我们可以选取适量的卡片拼接成几何图形．（卡片间不重叠、无缝隙）

根据已有的学习经验，解决下列问题：

（1）图1是由1张Ⅰ号卡片、1张Ⅱ号卡片、2张Ⅲ号卡片拼接成的正方形，那么这个几何图形表示的等式是（a+b）2=a2+2ab+b2；
（2）小聪想用几何图形表示等式2a2+3ab+b2=（a+b）（2a+b），图2给出了他所拼接的几何图形的一部分，请你补全图形；
（3）小聪选取2张Ⅰ号卡片、2张Ⅱ号卡片、5张Ⅲ号卡片拼接成一个长方形，请你画出拼接的几何图形的长方形，并直接写出几何图形表示的等式．
7．已知a，b满足$\sqrt{4a-5b}$+$\sqrt{a-b-1}$=0，则$\sqrt{ab}$÷$\sqrt{\frac{{b}^{3}}{a}}$-b=-$\frac{11}{4}$．
14．如图，在平面直角坐标系中，点B（3，0），点C（0，4），四边形ABCD是菱形，对角线BD于y轴交于点P．
（1）请直接写出A点与D点坐标；
（2）动点M从B点出发以每秒1个单位的速度沿折线段B-A-D运动，设△AMP的面积为S（S≠0），运动时间为t（秒），求面积S与时间t之间的函数关系式，并直接写出自变量的取值范围；
（3）在（2）的条件下，是否存在一点M，使△DMP沿其一边翻折构成的四边形是菱形？若存在，求出点M的坐标；若不存在，请说明理由．
4．计算（-a+2b）2-（-a-2b）2的结果是（　　）
A．-8abB．-4abC．8abD．4ab
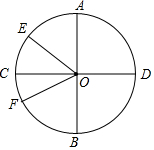11．如图，圆O的直径为10cm，两条直径AB，CD相交成90°角，∠AOE=50°，OF是∠BOE的平分线．
（1）求圆心角∠COF的度数；
（2）求扇形COF的面积．
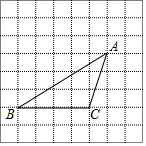8．如图，将方格纸中的三角形ABC先向右平移2格得到三角形DEF，再将三角形DEF向上平移3格得到三角形GPH．
（1）动手操作：按上面步骤画出经过两次平移后分别得到的三角形．
（2）写出图中与AC即平行又相等的一条线段DF，与∠BAC相等的一个角∠EDF．
9．观察下列各式：（x-1）（x+1）=x2-1（x-1）（x2+x+1）=x3-1（x-1）（x3+x2+x+1）=x4-1
…
（1）根据以上规律，（x-1）（x8+x7+x6+x5+x4+x3+x2+x+1）=x9-1；
（2）你能否由此归纳出一个一般性规律：（x-1）（xn+xn-1+…+x+1）=xn+1-1；
（3）根据（2）的规律请你求出：1+2+22+…+22016+22017的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网