△ABC的三边之比为3:4:5.与其相似的△DEF的最短边是9cm.则其最长边的长是( )A．5 cmB．10 cmC．15 cmD．30 cm 题目和参考答案——青夏教育精英家教网—

题目内容

1．△ABC的三边之比为3：4：5，与其相似的△DEF的最短边是9cm，则其最长边的长是（　　）

A．

5 cm

B．

10 cm

C．

15 cm

D．

30 cm

分析由相似三角形的性质可求得△DEF的最短边和最长边的比为3：5，则可求得答案．

解答解：
∵△ABC和△DEF相似，
∴△DEF的三边之比为3：4：5，
∴△DEF的最短边和最长边的比为3：5，
设最长边为x，则3：5=9：x，解得x=15，
∴△DEF的最长边为15cm，
故选C．

点评本题主要考查相似三角形的性质，掌握相似三角形的边对应成比例是解题的关键．

练习册系列答案

相关题目

11．把多项式3x²-5-2x+x³按x的降幂排列是x³+3x²-2x-5．

12．关于x的方程$\frac{x-1}{x-2}$=$\frac{m}{x-1}$+1有增根，则m的值是（　　）

	A．	矩形的对角线相等
	B．	菱形的面积等于两条对角线乘积的一半
	C．	对角线互相垂直的矩形是正方形
	D．	有两个角相等的梯形是等腰梯形

16．今年，我省启动了“爱护眼睛保护视力”仪式，某小学为了了解各年级戴近视镜的情况，对一到六年级近视的学生进行了统计，得到每个年级的近视的儿童人数分别为20，30，20，34，36，40，对于这组数据，下列说法错误的是（　　）

1．

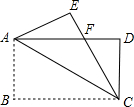如图，将矩形ABCD沿对角线AC对折，使△ABC落在△ACE的位置，且CE与AD相交于点F，连结ED，若AB=$\sqrt{3}$，BC=3．
（1）求证：AF=FC；
（2）求EF的长；
（3）求ED的长．

8．材料1：从三张不同卡片中选出两张后排成一列，有6种不同的排列：抽象成数学问题就是：从3个不同的元素中任取2个元素的排列，其排列数记为：A₃²=3×2=6，一般地A_n^m=n（n-1）（n-2）…（n-m+1）（m、n为正整数，且m≤n）
材料2：从三张不同卡片中选取两张，有3种不同的选法：抽象成数学问题就是：从3个不同的元素中选取2个元素的组合，其组合数为C₃²=$\frac{3×2}{2×1}$=3，一般地C_n^m=$\frac{n（n-1）（n-2）…（n-m+1）}{m（m-1）（m-2）×…×2×1}$（m、n为正整数，且m≤n）
由以上材料，你可以知道：从7个人中选取4人，排成一列，共有（　　）种不同的排法．

5．关于x的方程-x+k=$\frac{1}{x}$（-2＜k＜2）的解的个数是0个．

6．

如图，已知AB∥CD，BC平分∠ABE，∠C=29°，则∠BED的度数是（　　）

试题分类