题目内容
11.点A(1,m)在函数y=2x的图象上,则点A的坐标是(1,2).分析 直接把点A(1,m)代入函数y=2x,求出m的值即可.
解答 解:∵点A(1,m)在函数y=2x的图象上,
∴m=2.
则A(1,2).
故答案为:(1,2).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
2.若不等式组$\left\{\begin{array}{l}{1<x≤2}\\{x>a}\end{array}\right.$有解,则a的取值范围是( )
| A. | a<2 | B. | a<1 | C. | a≥2 | D. | 1≤a<2 |
6.下列各式从左到右的变形是因式分解的是( )
| A. | a(a-b+1)=a2-ab+a | B. | a2-a-2=a(a-1)-2 | C. | a2-b2=(a+b)(a-b) | D. | a2-4a-5=(a-2)2-9 |
1.表中给出A,B,C三种上宽带网的收费方式.
设月上网时间为x小时,方案A的收费金额为y1,方案B的收费金额为y2,方案C的收费金额为y3;
(Ⅰ)在方案A中,超时费一定会产生吗?如果不一定,请说明产生超时费的取值范围.
(Ⅱ)请直接写出y1,y2,y3关于x的函数关系式,并写出相应的自变量取值范围.
(Ⅲ)在什么情况下选择方式B最省钱?并说明理由.
| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
(Ⅰ)在方案A中,超时费一定会产生吗?如果不一定,请说明产生超时费的取值范围.
(Ⅱ)请直接写出y1,y2,y3关于x的函数关系式,并写出相应的自变量取值范围.
(Ⅲ)在什么情况下选择方式B最省钱?并说明理由.
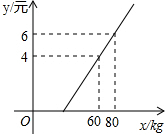 某航空公司规定旅客可随身携带一定质量的行李,如果超过规定则需要购买行李票,已知行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示,求y与x的函数解析式,并写出自变量x的取值范围.
某航空公司规定旅客可随身携带一定质量的行李,如果超过规定则需要购买行李票,已知行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示,求y与x的函数解析式,并写出自变量x的取值范围.