题目内容
3.(1)计算:(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$+($\sqrt{\frac{1}{3}}$)2.(2)$\sqrt{17}$的整数部分是a,小数部分是b,求-a2+|b2-1|-2ab的值.
分析 (1)原式利用二次根式的乘除法则及性质计算即可得到结果;
(2)根据题意估算出a与b,代入原式计算即可得到结果.
解答 解:(1)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$)÷2$\sqrt{3}$+$\frac{1}{3}$=3-$\frac{1}{3}$+2+$\frac{1}{3}$=5;
(2)∵16<17<25,
∴4<$\sqrt{17}$<5,
∴a=4,b=$\sqrt{17}$-4,
∴-a2+|b2-1|-2ab=-16+|32-8$\sqrt{17}$|-8($\sqrt{17}$-4)=-16.
点评 此题考查了二次根式的混合运算,以及估算无理数的大小,熟练掌握运算法则是解本题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
18.若∠1与∠2互补,∠2与∠3互余,且∠1=140°,则∠3等于( )
| A. | 40° | B. | 130° | C. | 50° | D. | 140° |
8.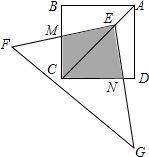 如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )
如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )
 如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )
如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )| A. | $\frac{5}{9}$a2 | B. | $\frac{4}{9}$a2 | C. | $\frac{2}{3}$a2 | D. | $\frac{1}{4}$a2 |
12.某商场推销某一运动服,先做了市场调查,得到销售量y(件)于每件售出价格x(元)的关系如下表.
(1)求y与x的函数关系式;
(2)若物价部门规定该商品的价格不能高于60元,且不能低于45元,商场将售价定为多少时,该商品的销量最大?
| 售出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量y(件) | 500 | 490 | 480 | 470 | … |
(2)若物价部门规定该商品的价格不能高于60元,且不能低于45元,商场将售价定为多少时,该商品的销量最大?