题目内容
 如图,在Rt△ABC中,∠C=90°,AB∥x轴且交抛物线y=ax2+bx+c于点A、B,交y轴于点D,设CD=m.
如图,在Rt△ABC中,∠C=90°,AB∥x轴且交抛物线y=ax2+bx+c于点A、B,交y轴于点D,设CD=m.(1)求a与m的关系式;
(2)若BC=2AC,求S△ABC(用含有a的式子表示),并求出b的值.
考点:二次函数的性质
专题:
分析:(1)求出△ACD和△CBD相似,根据相似三角形对应边成比例列式表示出AD•DB,再表示出点A、D的纵坐标,然后代入抛物线解析式得到关于x的一元二次方程,再利用根与系数的关系表示出AD•DB,整理即可得解;
(2)根据相似三角形对应边成比例表示出AD、DB,然后求出AB,再根据三角形的面积公式列式计算即可得解;利用根与系数的关系列式求解即可得到b的值.
(2)根据相似三角形对应边成比例表示出AD、DB,然后求出AB,再根据三角形的面积公式列式计算即可得解;利用根与系数的关系列式求解即可得到b的值.
解答:解:(1)∵AB∥x,
∴∠ADC=∠CDB=90°,
∴∠CAD+∠ACD=90°,
∵∠C=90°,
∴∠ACD+∠BCD=90°,
∴∠BCD=∠CAD,
∴△ACD∽△CBD,
∴
=
,
∴AD•DB=CD2=m2,
令x=0,则y=c,
∵CD=m,
∴点A、D的纵坐标为m+c,
∴ax2+bx+c=m+c,
∴ax2+bx-m=0,
∴AD•DB=-
,
∴-
=m2,
解得ma=1;
(2)由(1)知△ACD∽△CBD,
∴
=
=
,
∵BC=2AC,
∴
=
=
,
∴AD=
m,DB=2m,
∴AB=AD+DB=
m+2m=
,
∴S△ABC=
•
•m=
m2;
由根与系数的关系得,-AD+DB=-
,
∴-
m+2m=-
,
∴b=-
ma=-
.
∴∠ADC=∠CDB=90°,
∴∠CAD+∠ACD=90°,
∵∠C=90°,
∴∠ACD+∠BCD=90°,
∴∠BCD=∠CAD,
∴△ACD∽△CBD,
∴
| AD |
| CD |
| CD |
| DB |
∴AD•DB=CD2=m2,
令x=0,则y=c,
∵CD=m,
∴点A、D的纵坐标为m+c,
∴ax2+bx+c=m+c,
∴ax2+bx-m=0,
∴AD•DB=-
| -m |
| a |
∴-
| -m |
| a |
解得ma=1;
(2)由(1)知△ACD∽△CBD,
∴
| AD |
| CD |
| CD |
| DB |
| AC |
| BC |
∵BC=2AC,
∴
| AD |
| m |
| m |
| DB |
| 1 |
| 2 |
∴AD=
| 1 |
| 2 |
∴AB=AD+DB=
| 1 |
| 2 |
| 5m |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 5m |
| 2 |
| 5 |
| 4 |
由根与系数的关系得,-AD+DB=-
| b |
| a |
∴-
| 1 |
| 2 |
| b |
| a |
∴b=-
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了二次函数的性质,相似三角形的判定与性质,根与系数的关系,难点在于用相似三角形的性质和根与系数的关系两种方法表示出AD•DB.

练习册系列答案
相关题目
 如图,在矩形ADBC中,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,求点B到原点的最大距离.
如图,在矩形ADBC中,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,求点B到原点的最大距离.

 已知:如图,直线y=-
已知:如图,直线y=-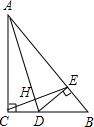 已知:如图,在△ABC中,∠ACB=90°,∠CAB的平分线交BC于D,DE⊥AB,垂足为E,连结CE,交AD于点H.
已知:如图,在△ABC中,∠ACB=90°,∠CAB的平分线交BC于D,DE⊥AB,垂足为E,连结CE,交AD于点H.