题目内容
 如图,在矩形ADBC中,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,求点B到原点的最大距离.
如图,在矩形ADBC中,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,求点B到原点的最大距离.考点:矩形的性质,线段的性质:两点之间线段最短,直角三角形斜边上的中线,勾股定理
专题:
分析:取AC的中点E,连接OE、BE、OB,根据三角形的任意两边之和大于第三边可知当O、B、E三点共线时,点B到点O的距离最大,再根据勾股定理列式求出BE的长,根据直角三角形斜边上的中线等于斜边的一半求出OE的长,两者相加即可得解.
解答: 解:如图,取AC的中点E,连接OE、BE、OB,
解:如图,取AC的中点E,连接OE、BE、OB,
∵OB<OE+BE,
∴当O、B、E三点共线时,点B到点O的距离最大,
∵AC=4,BC=2,
∴OE=AE=
AC=2,
在Rt△BCE中,由勾股定理得:BE=
=2
,
即点B到原点的最大距离是OE+BE=2+2
.
 解:如图,取AC的中点E,连接OE、BE、OB,
解:如图,取AC的中点E,连接OE、BE、OB,∵OB<OE+BE,
∴当O、B、E三点共线时,点B到点O的距离最大,
∵AC=4,BC=2,
∴OE=AE=
| 1 |
| 2 |
在Rt△BCE中,由勾股定理得:BE=
| 22+22 |
| 2 |
即点B到原点的最大距离是OE+BE=2+2
| 2 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,矩形的性质,勾股定理,根据三角形的三边关系判断出点O、B、E三点共线时,点B到点O的距离最大是解题的关键.

练习册系列答案
相关题目
当x=-2时,代数式x2-5的值为( )
| A、-9 | B、-3 | C、-1 | D、2 |
 如图,AB与CD交于点O,OE平分∠COB,BF∥OE,已知∠BOD=20°,则∠ABF=( )
如图,AB与CD交于点O,OE平分∠COB,BF∥OE,已知∠BOD=20°,则∠ABF=( )| A、100° | B、110° |
| C、120° | D、140° |
 如图,直线AB∥CD,AF交CD于点E,∠BED=30°,∠AEB=80°,则A=
如图,直线AB∥CD,AF交CD于点E,∠BED=30°,∠AEB=80°,则A=
 如图,在平面直角坐标系中,O为原点,点A、B的坐标分别为(4,0),(2,-6),将△OAB绕AB的中点旋转180°,点O落到点C的位置,抛物线经过点O、A、C,点D是该抛物线的顶点.
如图,在平面直角坐标系中,O为原点,点A、B的坐标分别为(4,0),(2,-6),将△OAB绕AB的中点旋转180°,点O落到点C的位置,抛物线经过点O、A、C,点D是该抛物线的顶点.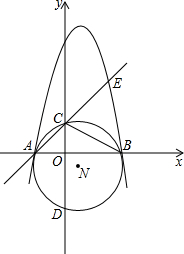 如图:抛物线y=x2+bx+c交x轴于A、B,直线y=x+2过点A,交y轴于C,交抛物线于E,且E的横坐标为3,△ABC的外接圆⊙N交y轴于另一点D.
如图:抛物线y=x2+bx+c交x轴于A、B,直线y=x+2过点A,交y轴于C,交抛物线于E,且E的横坐标为3,△ABC的外接圆⊙N交y轴于另一点D. 如图,在Rt△ABC中,∠C=90°,AB∥x轴且交抛物线y=ax2+bx+c于点A、B,交y轴于点D,设CD=m.
如图,在Rt△ABC中,∠C=90°,AB∥x轴且交抛物线y=ax2+bx+c于点A、B,交y轴于点D,设CD=m.