题目内容
如图①,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,O),OB=OC,tan∠ACO=

(1)求这个二次函数的表达式.
(2)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
(3)如图②,若点G(2,n)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,设P点横坐标为,△APG的面积为S,试确定S与t之间的函数关系式.
| 1 |
| 3 |

(1)求这个二次函数的表达式.
(2)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
(3)如图②,若点G(2,n)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,设P点横坐标为,△APG的面积为S,试确定S与t之间的函数关系式.
考点:二次函数综合题
专题:
分析:(1)由B点的坐标为(3,O),OB=OC,tan∠ACO=
,可求得点C与点A的坐标,然后利用待定系数法即可求得二次函数的解析式;
(2)首先根据题意画出图形,然后分别从当直线MN在x轴上方时,设圆的半径为R(R>0),与当直线MN在x轴下方时,设圆的半径为r(r>0),去分析求解即可求得答案;
(3)首先求得直线AG的解析式,即可求点G的坐标,然后表示出点P与Q的坐标,由S=S△APG=S△APQ+S△PGQ,即可求得答案.
| 1 |
| 3 |
(2)首先根据题意画出图形,然后分别从当直线MN在x轴上方时,设圆的半径为R(R>0),与当直线MN在x轴下方时,设圆的半径为r(r>0),去分析求解即可求得答案;
(3)首先求得直线AG的解析式,即可求点G的坐标,然后表示出点P与Q的坐标,由S=S△APG=S△APQ+S△PGQ,即可求得答案.
解答:解:(1)∵B点的坐标为(3,O),OB=OC,
∴点B(3,0),
∵tan∠ACO=
,
∴OA=1,
∴点A(-1,0),
∴
,
解得:
,
∴这个二次函数的表达式为:y=x2-2x-3.
 (2)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),
(2)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),
则N(R+1,R),
∴R=(R+1)2-2(R+1)-3,
解得:R=
(负值舍去),
∴R=
;
②当直线MN在x轴下方时,设圆的半径为r(r>0),
∴N(r+1,-r),
∴-r=(r+1)2-2(r+1)-3,
解得:r=
(负值舍去),
∴r=
,
∴圆的半径为:
或
;
 (3)过点P作PQ∥y轴,交AG于点Q,则P(t,t2-2t-3),
(3)过点P作PQ∥y轴,交AG于点Q,则P(t,t2-2t-3),
∵G(2,n)在此抛物线上,
∴n=22-2×2-3=-3,
设直线AG的解析式为:y=kx+b,
把A(-1,0),G(2,-3)代入y=kx+b得:
,
解得:
,
∴直线AG的解析式为:y=-x-1,
∴点Q(t,-t-1),
联立:
,
解得:
或
,
点G(2,-3),
∴PQ=(-t-1)-(t2-2t-3)=-t2+t+2,
∴S=S△APG=S△APQ+S△PGQ=
×(-t2+t+2)×[2-(-1)]=-
t2+
t+3.
∴点B(3,0),
∵tan∠ACO=
| 1 |
| 3 |
∴OA=1,
∴点A(-1,0),
∴
|
解得:
|
∴这个二次函数的表达式为:y=x2-2x-3.
 (2)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),
(2)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
∴R=(R+1)2-2(R+1)-3,
解得:R=
1±
| ||
| 2 |
∴R=
1+
| ||
| 2 |
②当直线MN在x轴下方时,设圆的半径为r(r>0),
∴N(r+1,-r),
∴-r=(r+1)2-2(r+1)-3,
解得:r=
-1±
| ||
| 2 |
∴r=
-1+
| ||
| 2 |
∴圆的半径为:
1+
| ||
| 2 |
-1+
| ||
| 2 |
 (3)过点P作PQ∥y轴,交AG于点Q,则P(t,t2-2t-3),
(3)过点P作PQ∥y轴,交AG于点Q,则P(t,t2-2t-3),∵G(2,n)在此抛物线上,
∴n=22-2×2-3=-3,
设直线AG的解析式为:y=kx+b,
把A(-1,0),G(2,-3)代入y=kx+b得:
|
解得:
|
∴直线AG的解析式为:y=-x-1,
∴点Q(t,-t-1),
联立:
|
解得:
|
|
点G(2,-3),
∴PQ=(-t-1)-(t2-2t-3)=-t2+t+2,
∴S=S△APG=S△APQ+S△PGQ=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
点评:此题考查了待定系数法求函数的解析式、切线的性质、二次函数的性质以及三角形的面积问题.此题难度较大,综合性较强,注意掌握辅助线的作法,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目
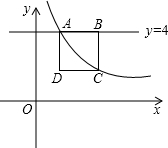 如图,直线y=4和反比例函数y=
如图,直线y=4和反比例函数y=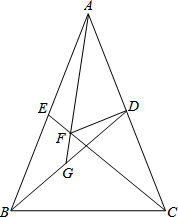 已知:如图,在△ABC中,AB=AC,点D、E分别是边AC、AB的中点,DF⊥AC,DF与CE相交于点F,AF的延长线与BD相交于点G.
已知:如图,在△ABC中,AB=AC,点D、E分别是边AC、AB的中点,DF⊥AC,DF与CE相交于点F,AF的延长线与BD相交于点G. 如图,BD是⊙O的直径,A是BD延长线上的一点,AC切⊙O于E,CB⊥AB于B,若AE:EC=2:1,DE+BE=4+2
如图,BD是⊙O的直径,A是BD延长线上的一点,AC切⊙O于E,CB⊥AB于B,若AE:EC=2:1,DE+BE=4+2 如图,在Rt△ABC中,∠C=90°,AB∥x轴且交抛物线y=ax2+bx+c于点A、B,交y轴于点D,设CD=m.
如图,在Rt△ABC中,∠C=90°,AB∥x轴且交抛物线y=ax2+bx+c于点A、B,交y轴于点D,设CD=m.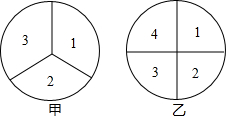 如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小军和小亮利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,转盘甲所指数字作为被除数,转盘乙所指数字作为除数,如果商大于1,小军获胜,否则小亮获胜,(当指针恰好停在分格线上时视为无效,重转).
如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小军和小亮利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,转盘甲所指数字作为被除数,转盘乙所指数字作为除数,如果商大于1,小军获胜,否则小亮获胜,(当指针恰好停在分格线上时视为无效,重转).