题目内容
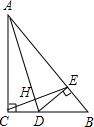已知：如图，在△ABC中，∠ACB=90°，∠CAB的平分线交BC于D，DE⊥AB，垂足为E，连结CE，交AD于点H．（1）求证：AD⊥CE；
（2）如果过点E作EF∥BC交AD于点F，连结CF，猜想四边形是什么图形？并证明你的猜想．
考点：全等三角形的判定与性质,菱形的判定
专题：
分析：（1）欲证明AD⊥CE，只需证得△ACE为等腰三角形；
（2）四边形CDEF是菱形．由（1）的结论结合已知条件可以推知对角线FD、CE相互垂直平分．
（2）四边形CDEF是菱形．由（1）的结论结合已知条件可以推知对角线FD、CE相互垂直平分．
解答：
证明：（1）如图，∵∠ACB=90°，∠CAB的平分线交BC于D，DE⊥AB，
∴在△ACD与△AED中，
，
∴△ACD≌△AED（AAS），
∴AC=AE，
∴AH⊥CE，即AD⊥CE；
（2）四边形CDEF是菱形．理由如下：
∵由（1）知，AC=AE，AD⊥CE，
∴CH=EH，
∵EF∥BC，
∴
=
，
∴FH=HD，
∴四边形CDEF是菱形．
证明：（1）如图，∵∠ACB=90°，∠CAB的平分线交BC于D，DE⊥AB，∴在△ACD与△AED中，
|
∴△ACD≌△AED（AAS），
∴AC=AE，
∴AH⊥CE，即AD⊥CE；
（2）四边形CDEF是菱形．理由如下：
∵由（1）知，AC=AE，AD⊥CE，
∴CH=EH，
∵EF∥BC，
∴
| EH |
| CH |
| FH |
| HD |
∴FH=HD，
∴四边形CDEF是菱形．
点评：此题主要考查了全等三角形的判定与性质，菱形与平行四边形的判定，以及角平分线的性质，题目综合性较强，关键是需要同学们熟练掌握基础知识．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，AB∥x轴且交抛物线y=ax2+bx+c于点A、B，交y轴于点D，设CD=m．若一个二次函数y=ax2-4ax+3（a≠0）的图象经过两点A（m+2，y1）、B（2-m，y2），则下列关系正确的是（ ）
| A、y1＞y2 |
| B、y1＜y2 |
| C、y1=y2 |
| D、y1≥y2 |
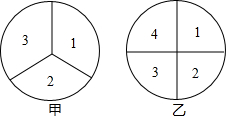如图是两个可以自由转动的转盘，甲转盘被等分成3个扇形，乙转盘被等分成4个扇形，每一个扇形上都标有相应的数字，小军和小亮利用它们做游戏，游戏规则是：同时转动两个转盘，当转盘停止后，转盘甲所指数字作为被除数，转盘乙所指数字作为除数，如果商大于1，小军获胜，否则小亮获胜，（当指针恰好停在分格线上时视为无效，重转）．