题目内容
7.计算题(1)($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)-($\sqrt{2}$-1)2
(2)2$\sqrt{3}$($\sqrt{12}$-3$\sqrt{75}$+$\frac{1}{3}$$\sqrt{108}$)
(3)已知:x为奇数,且$\sqrt{\frac{x-6}{9-x}}$=$\frac{\sqrt{x-6}}{\sqrt{9-x}}$,求$\sqrt{{x}^{2}-2x+1}$+$\sqrt{3x-1}$的值.
分析 (1)先根据乘法公式计算,然后合并同类二次根式即可;
(2)先化简二次根式,合并二次根式,再根据乘法计算方法计算即可;
(3)根据题意求得x的值,代入$\sqrt{{x}^{2}-2x+1}$+$\sqrt{3x-1}$计算即可.
解答 解:(1)原式=3-2-(3-2$\sqrt{2}$)
=2$\sqrt{2}$-2.
(2)原式=2$\sqrt{3}$(2$\sqrt{3}$-15$\sqrt{3}$+2$\sqrt{3}$)
=-2$\sqrt{3}$•11$\sqrt{3}$
=-66.
(3)由题意可知:6≤x<9,且x为奇数,则x=7,
$\sqrt{{x}^{2}-2x+1}$+$\sqrt{3x-1}$=6+2$\sqrt{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
15.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{0.34}$ | B. | $\sqrt{\frac{2}{5}}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\sqrt{7a{b}^{2}}$ |
19.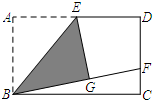 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )
 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )| A. | 6$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 4$\sqrt{6}$ |