题目内容
17.观察下面的一列数,按某种规律在横线上填上适当的数.2、5、9、14、20、27、35、…
分析 设该数列中第n个数为an(n为正整数),依次找出相邻两数的差(后面的数减前面的数),根据差的变化找出变化规律,依此规律即可得出结论.
解答 解:设该数列中第n个数为an(n为正整数),
观察,发现规律:a2-a1=5-2=3,a3-a2=9-5=4,a4-a3=14-9=5,a5-a4=20-14=6,…,
∴an+1-an=n+2,
∴a6=a5+7=20+7=27.
故答案为:27.
点评 本题考查了规律型中的数字的变化类,解题的关键是找出变化规律“an+1-an=n+2”.本题属于基础题,难度不大,解决该题型题目时,通过做差找出相邻两个数据之差的变化规律是关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
8.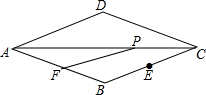 如图,菱形ABCD中,∠D=135°,AD=6,CE=2$\sqrt{2}$,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )
如图,菱形ABCD中,∠D=135°,AD=6,CE=2$\sqrt{2}$,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )
 如图,菱形ABCD中,∠D=135°,AD=6,CE=2$\sqrt{2}$,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )
如图,菱形ABCD中,∠D=135°,AD=6,CE=2$\sqrt{2}$,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )| A. | 3 | B. | 6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
5.下列计算正确的是( )
| A. | 3-1=-3 | B. | (a4)2=a8 | C. | a6÷a2=a3 | D. | $\sqrt{5}$-$\sqrt{2}$=$\sqrt{3}$ |
2.下列各式:$\frac{a-b}{2}$,$\frac{x+3}{x}$,$\frac{a+b}{a-b}$,$\frac{1}{m}$(x-y)中,是分式的共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.实数x取任何值,下列代数式都有意义的是( )
| A. | $\sqrt{6+2x}$ | B. | $\sqrt{2-x}$ | C. | $\sqrt{(x-1)^{2}}$ | D. | $\frac{\sqrt{x+1}}{x}$ |
5.某校准备去楠溪江某景点春游,旅行社面向学生推出的收费标准如下:
已知该校七年级参加春游学生人数多于100人,八年级参加春游学生人数少于100人.经核算,若两个年级分别组团共需花费17700元,若两个年级联合组团只需花费14700元.
(1)两个年级参加春游学生人数之和超过200人吗?为什么?
(2)两个年级参加春游学生各有多少人?
| 人数m | 0<m≤100 | 100<m≤200 | m>200 |
| 收费标准(元/人) | 90 | 80 | 70 |
(1)两个年级参加春游学生人数之和超过200人吗?为什么?
(2)两个年级参加春游学生各有多少人?