题目内容
10.(1)如图1,已知正方形ABCD,E是AD上一点,F是BC上一点,G是AB上一点,H是CD上一点,线段EF、GH交于点O,∠EOH=∠C,求证:EF=GH;(2)如图2,若将正方形ABCD改为矩形ABCD,且AD=mAB其他条件不变,探索线段EF与线段GH的关系并加以证明;
(3)根据前面的探究,你能否将本题推广到一般平行四边形情况?若能,写出推广命题,画出图形,直接写出结论;若不能,简要说明理由.

分析 (1)可通过构建全等三角形来求解.分别过G、F作GN∥AD,FM∥CD,那么FM=GN,∠EMF=∠GNH=90°,而∠OGN和∠OFM都是等角的余角,因此△GNH≌△FME,那么可通过全等三角形得出GH=EF;
(2)方法同(1)都是分别过G、F作AD、CD的垂线,根据∠GOF=∠A,得出△HGN和△EFM中的∠HGN和∠EFM相等,然后再得出相似求出即可;
(3)方法同(1)都是分别过G、F作AD、CD的垂线,根据∠GOF=∠A,得出△HGN和△EFM中的∠HGN和∠EFM相等,然后再得出相似求出即可.
解答 (1)证明:如图1,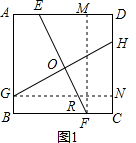
过点F作FM⊥AD于M,过点G作GN⊥CD于N,
则FM=GN=AD=BC,且GN⊥FM,设它们的垂足为Q,设EF、GN交于R
∵∠GOF=∠A=90°,
∴∠OGR=90°-∠GRO=90°-∠QRF=∠OFM.
在△GNH和△FME中
∵$\left\{\begin{array}{l}{∠HGN=∠EFM}\\{GN=MF}\\{∠GNH=∠FME}\end{array}\right.$
∴△GNH≌△FME(ASA).
∴EF=GH.
(2)解:$\frac{GH}{EF}$=$\frac{GN}{FM}$=m,
理由:如图2,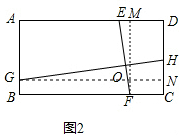
过点F作FM⊥AD于M,过点G作GN⊥CD于N,
设EF、GN交于R、GN、MF交于Q,
∵∠GOF=∠A=90°,
∴∠OGR=90-∠GRO=90-∠QRF=∠OFM.
∵∠GNH=∠FME=90°,
∴△GNH∽△FME.
∴$\frac{GH}{EF}$=$\frac{GN}{FM}$=m;
(3)已知平行四边形ABCD,E是AD上一点,F是BC上一点,G是AB上一点,
H是CD上一点,线段EF、GH交于点O,∠EOH=∠C,AD=mAB,则GH=mEF.
证明:如图3,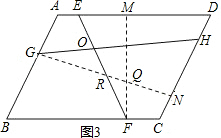
过点F作FM⊥AD于M,过点G作GN⊥CD于N,设EF、GN交于R、GN、MF交于Q,
在四边形MQND中,∠QMD=∠QND=90°,
∴∠MDN+∠MQN=180°.
∴∠MQN=∠A=∠GOF.
∵∠ORG=∠QRF,
∴∠HGN=∠EFM.
∵∠FME=∠GNH=90°,
∴△GNH∽△FME.
∴$\frac{GH}{EF}$=$\frac{GN}{FM}$=m.
即GH=mEF.
点评 本题主要考查了全等三角形和相似三角形的判定以及四边形综合等知识,构建出相关的三角形是解题的关键.

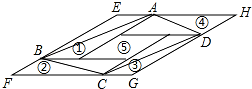 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定甲、乙的成绩谁更稳定 |
 如图,点B、C、E在同一条直线上,请你写出一个能使AB∥CD成立的条件:∠1=∠2.(只写一个即可,不添加任何字母或数字)
如图,点B、C、E在同一条直线上,请你写出一个能使AB∥CD成立的条件:∠1=∠2.(只写一个即可,不添加任何字母或数字)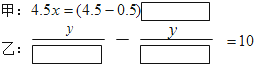
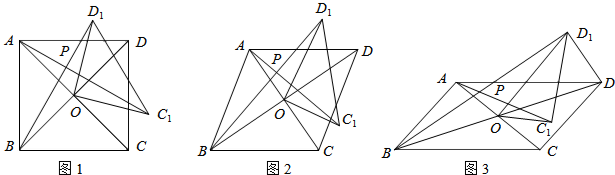
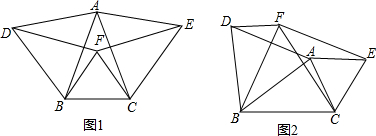
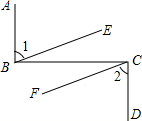 已知:如图,AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF.
已知:如图,AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF.