题目内容
5.已知a、b是一元二次方程x2-3x-2=0的两根,那么$\frac{1}{a}$+$\frac{1}{b}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
分析 根据$\frac{1}{a}+\frac{1}{b}=\frac{b}{ab}+\frac{a}{ab}=\frac{a+b}{ab}$,由一元二次方程的根与系数之间的关系求得两根之积与两根之和,代入数值计算即可
解答 解:∵方程x2-3x-2=0的两根为a,b,
∴a+b=3,ab=-2,
∴$\frac{1}{a}+\frac{1}{b}=\frac{b}{ab}+\frac{a}{ab}=\frac{a+b}{ab}$=$-\frac{3}{2}$.
故选:D.
点评 此题考查了一元二次方程根与系数的关系的知识,注意若二次项系数不为1,x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,掌握根与系数的关系是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在平面直角坐标系中,已知O是原点,四边形ABCD是长方形,A,B,C的坐标分别为A(-3,1),B(-3,3),C(2,3).
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
(3)平移(2)中长方形ABCD,几秒钟后△OBD的面积等于长方形ABCD的面积.
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
| 点 | D | A1 | B1 | C1 | D1 |
| 坐标 |
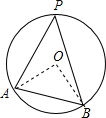 如图,A、B、P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为2$\sqrt{2}$.
如图,A、B、P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为2$\sqrt{2}$.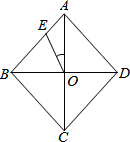 如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,求∠EOA的度数.
如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,求∠EOA的度数.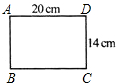 如图,木工师傅要以旧翻新一张桌面,打算把一块长宽为20cm和14cm的矩形桌面ABCD的四个角锯成半径为5cm,并且与两边相切的圆弧形.请你在木板上把其中一个角的圆弧线画出来(要求尺规作图,保留画图痕迹),并求出新桌面面积.
如图,木工师傅要以旧翻新一张桌面,打算把一块长宽为20cm和14cm的矩形桌面ABCD的四个角锯成半径为5cm,并且与两边相切的圆弧形.请你在木板上把其中一个角的圆弧线画出来(要求尺规作图,保留画图痕迹),并求出新桌面面积. 多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.
多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.