题目内容
17. 多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.
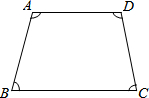
多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.例如:如图四边形ABCD的内角和:
N=∠A+∠B+∠C+∠D=(4-2)×180°=360°
问:(1)利用这个关系式计算五边形的内角和;
(2)当一个多边形的内角和N=720°时,求其边数n.
分析 (1)将n=5代入公式,依据公式计算即可;
(2)将N=720°代入公式,得到关于n的方程,然后求解即可.
解答 解:(1)N=(5-2)×180°=540°
(2)根据题意得:(n-2)×180°=720°
解得n=6.
点评 本题主要考查的是多边形的内角和公式的应用,掌握多边形的内角和公式是解题的关键.

练习册系列答案
相关题目
7.下列运算正确的是( )
| A. | 2(2x-3)=4x-3 | B. | 2x+3x=5x2 | C. | (x+1)2=x2+1 | D. | $\frac{1}{a-b}$+$\frac{1}{b-a}$=0 |
5.已知a、b是一元二次方程x2-3x-2=0的两根,那么$\frac{1}{a}$+$\frac{1}{b}$的值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
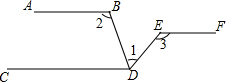 如图所示,已知AB∥CD∥EF,请问∠1、∠2、∠3之间有什么数量关系?请写出推理过程,并在每一步后面写上依据.
如图所示,已知AB∥CD∥EF,请问∠1、∠2、∠3之间有什么数量关系?请写出推理过程,并在每一步后面写上依据.