题目内容
16.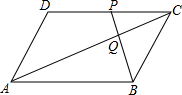 如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.
如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.(1)求证:△ABQ∽△CPQ;
(2)若△CPQ的周长为6,面积为4,求出△ABQ的周长和面积.
分析 (1)由相似三角形的判定可直接得出;
(2)根据相似三角形的性质:相似三角形周长的比等于相似比,面积比等于相似比的平方直接得出.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD
∴△ABQ∽△CPQ;
(2)解:∵四边形ABCD是平行四边形,点P是CD的中点,
∴AB=CD=2CP,
∴$\frac{AB}{CP}=2$,
∵△ABQ∽△CPQ,
∴$\frac{△ABQ的周长}{△CPQ的周长}$=$\frac{AB}{CP}$=2,
$\frac{△ABQ的面积}{△CPQ的面积}=(\frac{AB}{CP})^{2}$=4,
即$\frac{△ABQ的周长}{6}=2$.
$\frac{△ABQ的面积}{4}=4$,
∴△ABQ的周长=12,
△ABQ的面积=16.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,F、G分别是AB、AC的中点,DF⊥AB交BC于点D,EG⊥AC交AC于点G,BC=10,求△ADE周长.
如图,在△ABC中,F、G分别是AB、AC的中点,DF⊥AB交BC于点D,EG⊥AC交AC于点G,BC=10,求△ADE周长.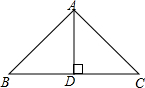 如图是小磊制作的一个三角形钢架模型ABC,其中BC=xcm,且BC+AD=40cm,设△ABC的面积为Scm2
如图是小磊制作的一个三角形钢架模型ABC,其中BC=xcm,且BC+AD=40cm,设△ABC的面积为Scm2 如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB,CD的位置关系如何?
如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB,CD的位置关系如何? 如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.
如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.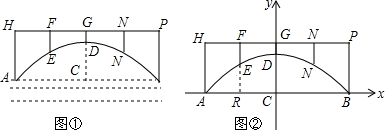
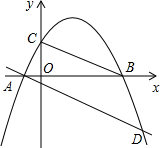 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°.