题目内容
7.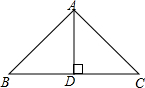 如图是小磊制作的一个三角形钢架模型ABC,其中BC=xcm,且BC+AD=40cm,设△ABC的面积为Scm2
如图是小磊制作的一个三角形钢架模型ABC,其中BC=xcm,且BC+AD=40cm,设△ABC的面积为Scm2(1)求出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,这个三角形的面积S最大?最大面积是多少?
分析 (1)BC=xcm,且BC+AD=40cm,可表示出这边上的高AD=40-x,然后利用三角形的面积公式列式整理出S与x之间的函数关系式;
(2)根据二次函数的最值问题解答.
解答 解:BC=xcm,且BC+AD=40cm,
∴高AD=(40-x)cm,
∴S=$\frac{1}{2}$(40-x)x=-$\frac{1}{2}$x2+20x;
(2)S=-$\frac{1}{2}$x2+20x
=-$\frac{1}{2}$(x-20)2+200,
∵-$\frac{1}{2}$<0,
∴x=20时,三角形的面积有最大值为200cm2.
点评 本题考查了二次函数的最值问题,主要利用了三角形的面积,整理出二次函数的顶点式解析式的形式是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.有一拦水坝的横截面是等腰梯形,它的上底为6米,下底为10米,高为2米,那么拦水坝斜坡的坡度和坡角分别是( )
| A. | $\frac{\sqrt{3}}{3}$,60° | B. | 1,45° | C. | $\sqrt{3}$,60° | D. | $\frac{\sqrt{3}}{3}$,30° |
2.作函数y=-x2的图象,并根据图象回答问题.
(1)列表:
(2)描点作图:
(3)函数y=-x2的图象是一条抛物线,开口向下,对称轴为y(x或y)轴,顶点坐标是(0,0),函数有最大(大或小)值0.
(4)在函数y=-x2中,当x>0时,若x1>x2,函数值y1<y2;当x<0时,若x1>x2,函数值y1>y2.
(1)列表:
| x | … | -3 | 0 | 1 | 2 | … | |||
| y=-x2 | … | -4 | -1 | -9 | … |

(3)函数y=-x2的图象是一条抛物线,开口向下,对称轴为y(x或y)轴,顶点坐标是(0,0),函数有最大(大或小)值0.
(4)在函数y=-x2中,当x>0时,若x1>x2,函数值y1<y2;当x<0时,若x1>x2,函数值y1>y2.
17.试根据表格中对应值解答下列问题:
(1)用代数式表示所挂质量为xkg的物体(在弹性限度内)时的弹簧的长度l;
(2)所挂物体的质量为10kg时,弹簧的长度是多少;
(3)若测得弹簧的长度是18cm,则所挂物体的质量为多少?
| 悬挂物体的质量x/kg | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 弹簧的长度l/cm | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15.5 | 16 | … |
(2)所挂物体的质量为10kg时,弹簧的长度是多少;
(3)若测得弹簧的长度是18cm,则所挂物体的质量为多少?
 如图,在梯形ABCD中,AD∥BC,AB=DC,BC=AC,∠ACD=30°,则∠D=110°.
如图,在梯形ABCD中,AD∥BC,AB=DC,BC=AC,∠ACD=30°,则∠D=110°.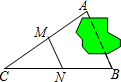 A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m.
A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m. 如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.
如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.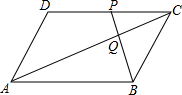 如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.
如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.