题目内容
11. 如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.
如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.
分析 由四边形ABCD是平行四边形,可得AB∥DC,AD∥BC,即可证得△ABF∽△EDF,△AFO∽△BCO,根据相似三角形的性质得到$\frac{AO}{CO}=\frac{BO}{OE}$,$\frac{OF}{BO}=\frac{AO}{OC}$,等量代换得到$\frac{BO}{OE}=\frac{OF}{OB}$,即可得到结论.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴△ABO∽△CEO,△AFO∽△BCO,
∴$\frac{AO}{CO}=\frac{BO}{OE}$,$\frac{OF}{BO}=\frac{AO}{OC}$,
∴$\frac{BO}{OE}=\frac{OF}{OB}$,
∴$\frac{BO}{FO}$=$\frac{EO}{BO}$.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
2.作函数y=-x2的图象,并根据图象回答问题.
(1)列表:
(2)描点作图:
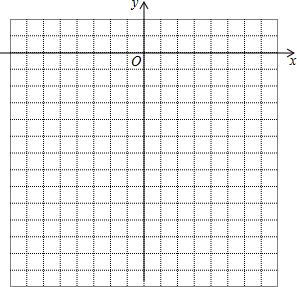
(3)函数y=-x2的图象是一条抛物线,开口向下,对称轴为y(x或y)轴,顶点坐标是(0,0),函数有最大(大或小)值0.
(4)在函数y=-x2中,当x>0时,若x1>x2,函数值y1<y2;当x<0时,若x1>x2,函数值y1>y2.
(1)列表:
| x | … | -3 | 0 | 1 | 2 | … | |||
| y=-x2 | … | -4 | -1 | -9 | … |

(3)函数y=-x2的图象是一条抛物线,开口向下,对称轴为y(x或y)轴,顶点坐标是(0,0),函数有最大(大或小)值0.
(4)在函数y=-x2中,当x>0时,若x1>x2,函数值y1<y2;当x<0时,若x1>x2,函数值y1>y2.
1.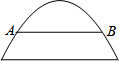 如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )
如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )
 如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )
如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )| A. | 5m | B. | 6m | C. | $\sqrt{6}$m | D. | 2$\sqrt{6}$m |

 如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.
如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.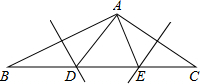 如图,在△ABC中,已知AB,AC的垂直平分线分别交BC于点D,E,且∠BAC=125°,则∠DAE是70度.
如图,在△ABC中,已知AB,AC的垂直平分线分别交BC于点D,E,且∠BAC=125°,则∠DAE是70度.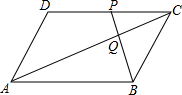 如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.
如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.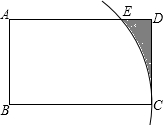 如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.
如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.