题目内容
1.图中的图①是座抛物线形拱桥的示意图,相邻两支柱间的距离为10米(即HF=FG=GM=MP=10米),拱桥顶点D到桥面的距离DG=2米,将桥拱置于如图②所示的平面直角坐标系中,抛物线的解析式为y=ax2+6.(1)求a的值;
(2)求支柱EF的高.
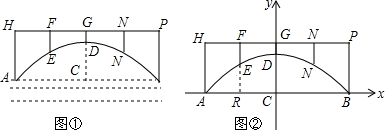
分析 (1)根据题意可知顶点D(0,6),A(-20,0),代入y=ax2+6可求出a的值;
(2)把x=-10代入函数表达式即可求出点E的纵坐标,即可求出EF的长.
解答 解:(1)根据题意可知顶点D(0,6),A(-20,0),
∴0=400a+6
∴a=-$\frac{3}{200}$;
(2)把x=-10代入y=-$\frac{3}{200}$x2+6,
y=-$\frac{3}{2}$+6=$\frac{9}{2}$
∴EF=8-$\frac{9}{2}$=$\frac{7}{2}$.
点评 此题主要考查了二次函数的应用,利用图象得出函数解析式的性质以及各点坐标是解题关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13.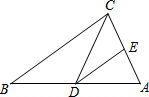 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )
 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )| A. | △ADE∽△ABC | B. | △ADE∽△ACD | C. | △DEC∽△CDB | D. | △ADE∽△DCB |
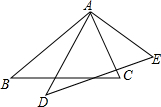 如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度.
如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度. A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m.
A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m.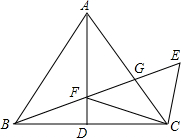 如图,△ABC中,AB=AC,点D为BC边中点,CE∥AB,BE分别交AD、AC于点F、G,连接FC.求证:
如图,△ABC中,AB=AC,点D为BC边中点,CE∥AB,BE分别交AD、AC于点F、G,连接FC.求证: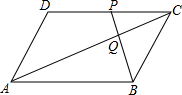 如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.
如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.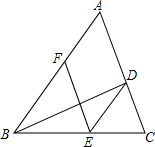 如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,EF∥AC.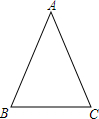 如图,△ABC中,AB=AC=13,BC=10
如图,△ABC中,AB=AC=13,BC=10