题目内容
4. 如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB,CD的位置关系如何?
如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB,CD的位置关系如何?
分析 运用角平分线的定义,结合图形可知∠ABD=2∠1,∠BDC=2∠2,又已知∠1+∠2=90°,可得同旁内角∠ABD和∠BDC互补,从而证得AB∥CD.
解答 解:∵BE平分∠ABD,DE平分∠BDC(已知),
∴∠ABD=2∠1,∠BDC=2∠2(角平分线定义),
∵∠1+∠2=90°,
∴∠ABD+∠BDC=2(∠1+∠2)=180°,
∴AB∥CD(同旁内角互补,两直线平行).
点评 本题考查平行线的判定和角平分线的定义.灵活运用角平分线的定义和角的和差的关系是解决本题的关键,注意正确识别“三线八角”中的同位角、内错角、同旁内角.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
13.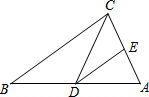 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )
 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,且∠DCE=∠B.那么下列各判断中,错误的是( )| A. | △ADE∽△ABC | B. | △ADE∽△ACD | C. | △DEC∽△CDB | D. | △ADE∽△DCB |
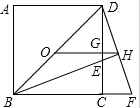 已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG. 如图,在梯形ABCD中,AD∥BC,AB=DC,BC=AC,∠ACD=30°,则∠D=110°.
如图,在梯形ABCD中,AD∥BC,AB=DC,BC=AC,∠ACD=30°,则∠D=110°.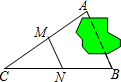 A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m.
A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m. 如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.
如图,已知DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,求∠B的度数.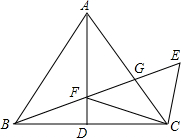 如图,△ABC中,AB=AC,点D为BC边中点,CE∥AB,BE分别交AD、AC于点F、G,连接FC.求证:
如图,△ABC中,AB=AC,点D为BC边中点,CE∥AB,BE分别交AD、AC于点F、G,连接FC.求证: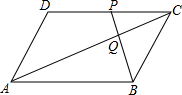 如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q.
如图,平行四边形ABCD中,点P是CD的中点,AC与PB相交于点Q. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1,则BD的长为2.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1,则BD的长为2.