题目内容
2.如果等腰三角形的周长是19cm,一腰上的中线把三角形分成两个三角形,其周长之差是4cm,则这个等腰三角形的底边长是7cm或$\frac{23}{3}$cm.分析 根据题意画出图形,设等腰三角形的腰长为x,则底边长为19-2x,再根据两个三角形的周长差是4cm求出x的值即可.
解答 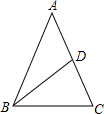 解:如图所示,等腰△ABC中,AB=AC,点D为AC的中点,设AB=AC=xcm,
解:如图所示,等腰△ABC中,AB=AC,点D为AC的中点,设AB=AC=xcm,
∵点D为AC的中点,
∴AD=CD=$\frac{x}{2}$,BC=25-(AB+AC)=19-2x,
当△ABD的周长大于△BCD的周长时,
AB+AD+BD-(BC+CD+BD)=4,即x+$\frac{x}{2}$-(19-2x)-$\frac{x}{2}$=4,解得x=$\frac{23}{3}$cm;
当△BCD的周长大于△ABD的周长时,
则BC+CD+BD-(AB+AD+BD)=4,即19-2x+$\frac{x}{2}$-(x+$\frac{x}{2}$)=4,解得x=5cm.
综上所述,这个等腰三角形的腰长为5cm或$\frac{23}{3}$cm.
故答案为:7cm或$\frac{23}{3}$cm.
点评 本题考查的是等腰三角形的性质,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知$\frac{1}{p}$=$\frac{v}{m}$-2,且p≠-$\frac{1}{2}$,则m=( )
| A. | $\frac{pv}{1+2p}$ | B. | $\frac{pv}{1-2p}$ | C. | $\frac{pv}{2p-1}$ | D. | $\frac{v-2}{p}$ |
11.二次函数 y=ax2+bx+2(a≠0)的图象经过点(-1,1),则代数式1-a+b的值为( )
| A. | -3 | B. | -1 | C. | 2 | D. | 5 |

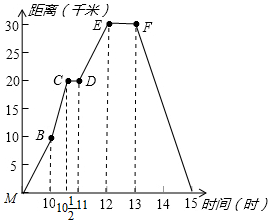 如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题:
如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题: