题目内容
12.已知a2-4a+1=0,求$\frac{{a}^{8}+1}{{a}^{4}}$的值.分析 先根据已知条件进行变形,利用完全平方公式可得:${a}^{4}+\frac{1}{{a}^{4}}$=194,再将所求的式子约分可得结论.
解答 解:a2-4a+1=0,
两边同时除以a,得:a-4+$\frac{1}{a}$=0,
∴a+$\frac{1}{a}$=4,
两边同时平方得:a2+2+$\frac{1}{{a}^{2}}$=16,
∴a2+$\frac{1}{{a}^{2}}$=14,
两边同时平方得:a4+2+$\frac{1}{{a}^{4}}$=196,
∴a4+$\frac{1}{{a}^{4}}$=194,
则$\frac{{a}^{8}+1}{{a}^{4}}$=a4+$\frac{1}{{a}^{4}}$=196.
点评 本题考查了分式的代入求值问题,本题有难度,不是直接将字母a的值代入,而是利用整体代入的思想,将已知条件进行变形,常采用方程两边同时除以一个数或式子的形式进行变形,或将原式变形为a2=4a-1,达到降次的目的.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
3.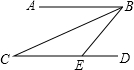 如图,AB∥CD,点E在CD上,BC平分∠ABE,若∠C=25°,则∠BED的度数是( )
如图,AB∥CD,点E在CD上,BC平分∠ABE,若∠C=25°,则∠BED的度数是( )
 如图,AB∥CD,点E在CD上,BC平分∠ABE,若∠C=25°,则∠BED的度数是( )
如图,AB∥CD,点E在CD上,BC平分∠ABE,若∠C=25°,则∠BED的度数是( )| A. | 25° | B. | 45° | C. | 50° | D. | 75° |
17.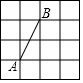 如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
 如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
 如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )



