题目内容
12.小明同学在做作业时,遇到这样一道几何题:
小明冥思苦想许久不得解,只好去问老师,老师给了他如下提示:
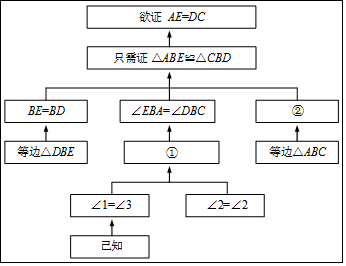
请问老师的提示中①是∠1+∠2=∠3+∠2,②是AB=BC.
分析 根据全等三角形的判定方法,等边三角形的性质,等量代换等知识即可解决问题.
解答 证明:∵△DBE、△ABC是等边三角形,
∴BE=BD,∠1=∠3=60°,AB=BC
∵∠1=∠3,∠2=∠2,
∴∠1+∠2=∠3+∠2,
∴∠EBA=∠DBC,
在△ABE和△CBD中,
$\left\{\begin{array}{l}{BE=BD}\\{∠EBA=∠DBC}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴AE=DC.
故答案为∠1+∠2=∠3+∠2,AB=BC.
点评 本考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,确定全等的条件,属于中考常考题型.

练习册系列答案
相关题目
15.-2的绝对值是( )
| A. | -2 | B. | 2 | C. | ±2 | D. | $-\frac{1}{2}$ |
16.下列各式中,正确的是( )
| A. | |-0.1|<0 | B. | $\frac{4}{3}$<-|-$\frac{5}{4}$| | C. | $\frac{6}{7}$>0.86 | D. | -2=-|-2| |
13. 如图,已知∠1=53°,要使AB∥CD,则∠2的余角的度数是( )
如图,已知∠1=53°,要使AB∥CD,则∠2的余角的度数是( )
 如图,已知∠1=53°,要使AB∥CD,则∠2的余角的度数是( )
如图,已知∠1=53°,要使AB∥CD,则∠2的余角的度数是( )| A. | 53° | B. | 37° | C. | 127° | D. | 143° |
7.某地中国移动“全球通”与“神州行”收费标准如下表:
如果小明每月拨打本地电话时间是长途电话时间的2倍,且每月总通话时间在65~70分钟之间,那么他选择全球通较为省钱(填“全球通”或“神州行”).
| 品牌 | 月租费 | 本地话费(元/分钟) | 长途话费(元/分钟) |
| 全球通 | 13元 | 0.35 | 0.15 |
| 神州行 | 0元 | 0.60 | 0.30 |
17.王先生清明节期间驾车游玩,每次加油都把油箱加满.如表记录了该车相邻两次加油时的相关数据:
注:“累计里程”指汽车从出厂开始累计行驶的路程.
根据数据,王先生计算出这段时间内该车行驶一百公里的平均耗油量大约是( )
| 加油时间 | 油箱加油量(升) | 加油时的累计里程(公里) |
| 2016年3月31日 | 30 | 87006 |
| 2016年4月3日 | 48 | 87606 |
根据数据,王先生计算出这段时间内该车行驶一百公里的平均耗油量大约是( )
| A. | 7升 | B. | 8升 | C. | 9升 | D. | 10升 |
