题目内容
17.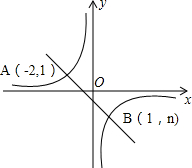 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件(1)求反比例函数与一次函数的关系式;
(2)根据图象写出使该一次函数的值大于该反比例函数的值的x的取值范围;
(3)求出△AOB的面积.
分析 (1)根据点A(-2,1)可以求得反比例函数的解析式,根据点B(1,n)在反比例函数上可以求得n的值,根据A、B的坐标可以求得一次函数的解析式;
(2)根据函数图象,可以得到一次函数的值大于该反比例函数的值的x的取值范围;
(3)根据直线与x交点和点A、B的坐标可以求得△AOB的面积.
解答 解:(1)由图可知,点A(-2,1),点B(1,n),
∵一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,
∴$1=\frac{m}{-2}$,得m=-2,
∴$n=\frac{-2}{1}$,得n=-2,
∴$\left\{\begin{array}{l}{-2k+b=1}\\{k+b=-2}\end{array}\right.$
解得,$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$
即反比例函数的解析式为$y=\frac{-2}{x}$,一次函数的解析式为y=-x-1;
(2)根据函数图象,一次函数的值大于该反比例函数的值的x的取值范围是x<-2或0<x<1;
(3)∵直线y=-x-1与x轴的交点坐标为(-1,0),
∴${S}_{△AOB}=\frac{|-1|×1}{2}+\frac{|-1|×|-2|}{2}$=$\frac{1}{2}+1$=$\frac{3}{2}$.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
7.下列命题中,属于真命题的是( )
| A. | 如果|a|>|b|,那么a2>b2 | B. | 如果a>b,那么a>-b | ||
| C. | 如果a<b,那么|a|<|b| | D. | 如果|a|=2,那么a=2 |
8.二次函数的部分对应值如下表:
由图可知该二次函数的图象对称轴为x=1,x=2对应的函数值y=-8.
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | 5 | 7 | … |
2.若x=-2,则x0、x-1、x-2之间的大小关系是( )
| A. | x0>x-2>x-1 | B. | x-2>x-1>x0 | C. | x0>x-1>x-2 | D. | x-1>x-2>x0 |
 小明家、学校与图书馆依次在一条直线上,小明、小亮两人同时分别从小明家和学校出发沿直线匀速步行到图书馆借阅图书,小明到达图书馆花了20分钟,小亮每分钟步行40米,小明离学校的距离y(米)与两人出发时间x(分)之间的函数图象如图所示.
小明家、学校与图书馆依次在一条直线上,小明、小亮两人同时分别从小明家和学校出发沿直线匀速步行到图书馆借阅图书,小明到达图书馆花了20分钟,小亮每分钟步行40米,小明离学校的距离y(米)与两人出发时间x(分)之间的函数图象如图所示.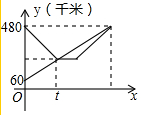 甲、乙两车分别从相距480千米的A、B两地出发,匀速相向行驶,乙车比甲车先出发1小时,从B地直达A地.甲车出发t小时两车相遇后甲车停留1小时,因有事按原路返回A地,两车同时到达A地.从甲车出发时开始计时,时间为x(时),甲、乙两车距B地的路程y(千米)与x(时)之间的函数关系如图所示
甲、乙两车分别从相距480千米的A、B两地出发,匀速相向行驶,乙车比甲车先出发1小时,从B地直达A地.甲车出发t小时两车相遇后甲车停留1小时,因有事按原路返回A地,两车同时到达A地.从甲车出发时开始计时,时间为x(时),甲、乙两车距B地的路程y(千米)与x(时)之间的函数关系如图所示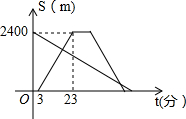 小红从劳动基地出发,步行返回学校,小军骑车从学校出发去劳动基地,在基地停留10分钟后,沿原路以原速返回,结果比小红早7分钟回到学校,若两人都是沿着同一路线行进,且两人与学校的距离s(米)和小红从劳动基地出发所用时间t(分)之间的函数关系如图所示,则下列说法中正确的结论有( )个
小红从劳动基地出发,步行返回学校,小军骑车从学校出发去劳动基地,在基地停留10分钟后,沿原路以原速返回,结果比小红早7分钟回到学校,若两人都是沿着同一路线行进,且两人与学校的距离s(米)和小红从劳动基地出发所用时间t(分)之间的函数关系如图所示,则下列说法中正确的结论有( )个