题目内容
7.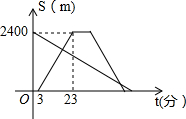 小红从劳动基地出发,步行返回学校,小军骑车从学校出发去劳动基地,在基地停留10分钟后,沿原路以原速返回,结果比小红早7分钟回到学校,若两人都是沿着同一路线行进,且两人与学校的距离s(米)和小红从劳动基地出发所用时间t(分)之间的函数关系如图所示,则下列说法中正确的结论有( )个
小红从劳动基地出发,步行返回学校,小军骑车从学校出发去劳动基地,在基地停留10分钟后,沿原路以原速返回,结果比小红早7分钟回到学校,若两人都是沿着同一路线行进,且两人与学校的距离s(米)和小红从劳动基地出发所用时间t(分)之间的函数关系如图所示,则下列说法中正确的结论有( )个①学校到劳动基地距离是2400米;
②小军出发53分钟后回到学校;
③小红的速度是40米/分;
④两人第一次相遇时距离学校1610米.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①令t=0,则S=2400,由此可知①正确;②根据速度=路程÷时间可算出小军的速度,由横坐标上的点可以知道小军往返的时间为2倍的(23-3)分钟,加上在劳动基地呆的10分钟可知小军出发50分钟后回到学校,②不正确;③由小军比小红早到校7分钟可知小红路上一共用了60分钟,由速度=路程÷时间可得出小红的速度,③正确;④由时间=路程÷速度和可算出相遇时小红出发的时间,由路程=速度×时间即可得出结论④不成立.结合上面分析即可得出结论.
解答 解:①令t=0,则S=2400,
∴学校到劳动基地距离是2400米,①正确;
②小军的速度为2400÷(23-3)=120(米/分),
小军到学校的时间为(23-3)+10+(23-3)=50(分钟),②不正确;
③小红到学校的时间为3+50+7=60(分钟),
小红的速度为2400÷60=40(米/分),③正确;
④两人第一次相遇的时间为3+(2400-3×40)÷(200+40)=12.5(分钟),
相遇的地点离学校的距离为2400-40×12.5=1900(米),④不正确.
综上可知只有①③正确.
故选B.
点评 本题考查了一次函数的应用,解题的关键是根据数量关系逐条分析4个结论.本题属于中档题,难度不大,解决该题型题目时,结合图形根据数量关系逐条分析数据是关键.

练习册系列答案
相关题目
18.下列计算正确的是( )
| A. | (-2a2)3=8a6 | B. | a3÷a2=a | C. | 2a2+a2=3a4 | D. | (a-b)2=a2-b2 |
15.某造纸厂生产甲、乙两种生活用纸的相关信息如下表,其中x(吨)表示甲、乙两种生活用纸的月产量,请根据表中的信息解答后面的问题:
(1)设该造纸厂每月生产甲、乙两种生活用纸的利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)若某月要生产甲、乙两种生活用纸共300吨,求该月生产甲、乙两种生活用纸各多少吨,获得的总利润最大?最大利润是多少?
| 种 品 价 目 | 出厂价(元/吨) | 成本价(元/吨) | 排污处理费 |
| 甲种生活用纸 | 4800 | 2200 | 200(元/吨) 每月还需支付设备管理、 维护费20000元 |
| 乙种生活用纸 | 7000-10x | 1600 | 400(元/吨) |
(2)若某月要生产甲、乙两种生活用纸共300吨,求该月生产甲、乙两种生活用纸各多少吨,获得的总利润最大?最大利润是多少?
2.函数y=-$\frac{6}{x}$的图象经过点A(x1,y1)、B(x2,y2),若x1<x2<0,则y1、y2、0三者的大小关系是( )
| A. | y1<y2<0 | B. | y2<y1<0 | C. | y1>y2>0 | D. | y2>y1>0 |
19.某天的最高气温是11℃,最低气温是-1℃,则这一天的最高气温与最低气温的差是( )
| A. | 2℃ | B. | -2℃ | C. | 12℃ | D. | -12℃ |
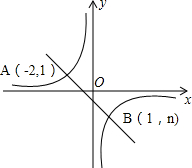 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件