题目内容
5.平行四边形ABCD的周长是56cm,对角线相交于点O,△BOC的周长比△AOB的周长小8cm,则AB=18cm,BC=10cm.分析 根据平行四边形的性质可知,平行四边形的对角线互相平分,对边相等,周长是56cm可得BC+AB=28cm,根据由于△BOC的周长比△AOB的周长小8cm,则AB比BC大8cm,继而可求出AB、BC的长度.
解答 解:∵?ABCD的周长为56cm,
∴BC+AB=28cm,①
又∵△BOC的周长比△AOB的周长小8cm,
∴AB-BC=8cm,②
由①②得
AB=18cm,BC=10cm.
故答案为:18,10.
点评 此题主要考查平行四边的性质:平行四边形的两组对边分别相等且平行四边形的对角线互相平分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元. 每辆车的月租金定为多少元时,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
| x | 4500 | 4000 | 3800 | 3200 |
| y | 70 | 80 | 84 | 96 |
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元. 每辆车的月租金定为多少元时,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
10.下列各题中,能用平方差公式的是( )
| A. | (a-2b)(-a+2b) | B. | (-a-2b)(-a-2b) | C. | (a-2b)(a+2b) | D. | (-a-2b)(a+2b) |
14.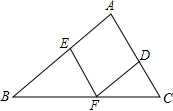 如图,在△ABC中,点D、E、F分别在边AC、AB、BC上,EF∥AC,DF∥AB,若∠B=45°,∠C=65°,则∠EFD的大小为( )
如图,在△ABC中,点D、E、F分别在边AC、AB、BC上,EF∥AC,DF∥AB,若∠B=45°,∠C=65°,则∠EFD的大小为( )
 如图,在△ABC中,点D、E、F分别在边AC、AB、BC上,EF∥AC,DF∥AB,若∠B=45°,∠C=65°,则∠EFD的大小为( )
如图,在△ABC中,点D、E、F分别在边AC、AB、BC上,EF∥AC,DF∥AB,若∠B=45°,∠C=65°,则∠EFD的大小为( )| A. | 45° | B. | 70° | C. | 80° | D. | 100° |
15.某造纸厂生产甲、乙两种生活用纸的相关信息如下表,其中x(吨)表示甲、乙两种生活用纸的月产量,请根据表中的信息解答后面的问题:
(1)设该造纸厂每月生产甲、乙两种生活用纸的利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)若某月要生产甲、乙两种生活用纸共300吨,求该月生产甲、乙两种生活用纸各多少吨,获得的总利润最大?最大利润是多少?
| 种 品 价 目 | 出厂价(元/吨) | 成本价(元/吨) | 排污处理费 |
| 甲种生活用纸 | 4800 | 2200 | 200(元/吨) 每月还需支付设备管理、 维护费20000元 |
| 乙种生活用纸 | 7000-10x | 1600 | 400(元/吨) |
(2)若某月要生产甲、乙两种生活用纸共300吨,求该月生产甲、乙两种生活用纸各多少吨,获得的总利润最大?最大利润是多少?
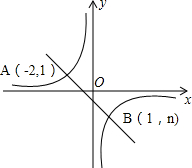 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件