题目内容
8.二次函数的部分对应值如下表:| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | 5 | 7 | … |
分析 ①由表格的数据可以看出,x=-3和x=5时y的值相同都是7,所以可以判断出,点(-3,7)和点(5,7)关于二次函数的对称轴对称,利用公式:x=$\frac{{x}_{1}+{x}_{2}}{2}$可求出对称轴;
②利用表格中数据反映出来的对称性,结合对称轴x=1,可判断出x=2时关于直线x=1对称的点为x=0,故可求出y=-8.
解答 解:①∵x=-3和x=5时,y=7,∴对称轴x=$\frac{-3+5}{2}$=1;
②x=2的点关于对称轴x=1对称的点为x=0,
∵x=0时,y=-8,
∴x=2时,y=-8,
故答案为1,-8.
点评 本题考查了二次函数的性质,要求掌握二次函数的对称性,会利用表格中的数据规律找到对称点,确定对称轴,再利用对称轴求得对称点.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
13.若x<1,那么$\sqrt{(x-1)^{2}}$+|5-x|等于( )
| A. | 6-2x | B. | 2x-6 | C. | 4 | D. | -4 |
3.下列式子是最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2{a^2}}$ | D. | $\sqrt{8}$ |
18.下列计算正确的是( )
| A. | (-2a2)3=8a6 | B. | a3÷a2=a | C. | 2a2+a2=3a4 | D. | (a-b)2=a2-b2 |
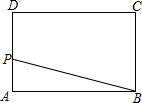 如图,P是矩形ABCD的边上的动点,当P从A点出发沿A→D→C→B运动到达B点时,△APB的面积s与运动时间t的函数关系的图象大致是( )
如图,P是矩形ABCD的边上的动点,当P从A点出发沿A→D→C→B运动到达B点时,△APB的面积s与运动时间t的函数关系的图象大致是( )

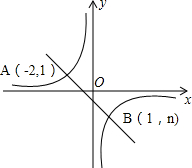 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件