题目内容
12.在Rt△ABC中,∠C=90°,∠A=30°,AB=4,则AC=2$\sqrt{3}$.分析 先利用含30度直角三角形的性质得到BC=$\frac{1}{2}$AB=2,再利用勾股定理求出AC的长即可.
解答  解:∵在Rt△ABC中,∠C=90°,∠A=30°,AB=4,
解:∵在Rt△ABC中,∠C=90°,∠A=30°,AB=4,
∴BC=$\frac{1}{2}$AB=2,
根据勾股定理得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 此题考查了含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.也考查了勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.下列式子是最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2{a^2}}$ | D. | $\sqrt{8}$ |
7.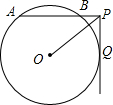 如图,⊙O中,点P是弦AB延长线上的一点,连接OP,过P作PQ⊥AP,且与⊙O相切于Q,若OP=4,∠APO=30°,则PA的长是( )
如图,⊙O中,点P是弦AB延长线上的一点,连接OP,过P作PQ⊥AP,且与⊙O相切于Q,若OP=4,∠APO=30°,则PA的长是( )
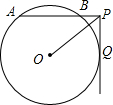 如图,⊙O中,点P是弦AB延长线上的一点,连接OP,过P作PQ⊥AP,且与⊙O相切于Q,若OP=4,∠APO=30°,则PA的长是( )
如图,⊙O中,点P是弦AB延长线上的一点,连接OP,过P作PQ⊥AP,且与⊙O相切于Q,若OP=4,∠APO=30°,则PA的长是( )| A. | 2$\sqrt{3}$+2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{13}$ | D. | $\sqrt{13}$ |
2.函数y=-$\frac{6}{x}$的图象经过点A(x1,y1)、B(x2,y2),若x1<x2<0,则y1、y2、0三者的大小关系是( )
| A. | y1<y2<0 | B. | y2<y1<0 | C. | y1>y2>0 | D. | y2>y1>0 |
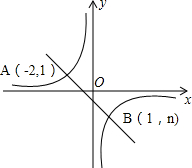 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点.利用图中条件