题目内容
8.观察下列各式(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
…
①根据以上规律,则(x-1)(x6+x5+x4+x3+x2+x+1)=x7-1.
②你能否由此归纳出一般性规律:(x-1)(xn+xn-1+…+x+1)=xn+1-1.
③根据②求出:1+2+22+…+234+235的结果.
分析 ①观察已知各式,得到一般性规律,化简原式即可;
②原式利用得出的规律化简即可得到结果;
③原式变形后,利用得出的规律化简即可得到结果.
解答 解:①根据题意得:(x-1)(x6+x5+x4+x3+x2+x+1)=x7-1;
②根据题意得:(x-1)(xn+xn-1+…+x+1)=xn+1-1;
③原式=(2-1)(1+2+22+…+234+235)=236-1.
故答案为:①x7-1;②xn+1-1;③236-1
点评 此题考查了多项式乘以多项式,弄清题中的规律是解本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.关于x的一元二次方程(m-1)x2-4mx+4m-2=0有实数根,则m满足的条件( )
| A. | m≤1 | B. | m≥1 | C. | m≥$\frac{1}{3}$且m≠1 | D. | -1<m≤1 |
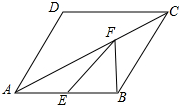 如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.
如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点. 如图,四边形ABCD是正方形,AC是一条对角线,阴影部分的面积和为16,则正方形ABCD的边长为4$\sqrt{2}$.
如图,四边形ABCD是正方形,AC是一条对角线,阴影部分的面积和为16,则正方形ABCD的边长为4$\sqrt{2}$.