题目内容
18. 如图,四边形ABCD是正方形,AC是一条对角线,阴影部分的面积和为16,则正方形ABCD的边长为4$\sqrt{2}$.
如图,四边形ABCD是正方形,AC是一条对角线,阴影部分的面积和为16,则正方形ABCD的边长为4$\sqrt{2}$.
分析 由正方形的性质和已知条件得出阴影部分的面积和=$\frac{1}{2}$正方形ABCD的面积,得出$\frac{1}{2}$AB2=16,即可求出AB的长.
解答 解:∵四边形ABCD是正方形,AC是对角线,
∴AB=BC=CD=DA,阴影部分的面积和=$\frac{1}{2}$正方形ABCD的面积,
∵阴影部分的面积和为16,
即$\frac{1}{2}$AB2=16,
∴AB2=32,
∴AB=$\sqrt{32}$=4$\sqrt{2}$;
故答案为:4$\sqrt{2}$.
点评 本题考查了正方形的性质、正方形的面积公式、阴影部分的面积;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
9. 如图,不能判定AB∥DF的是( )
如图,不能判定AB∥DF的是( )
 如图,不能判定AB∥DF的是( )
如图,不能判定AB∥DF的是( )| A. | ∠1=∠2 | B. | ∠A=∠4 | C. | ∠1=∠A | D. | ∠A+∠3=180° |
 如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=60°.
如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=60°.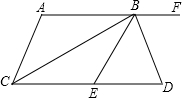 如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论: 如图,数轴上标出若干个点,每个相邻两点距离相等,点A,B,C,D对应的数分别是数a,b,c,d,a+b+c+d=2,a-b+c-d=-3,求a点位置.
如图,数轴上标出若干个点,每个相邻两点距离相等,点A,B,C,D对应的数分别是数a,b,c,d,a+b+c+d=2,a-b+c-d=-3,求a点位置.