题目内容
19.(1)计算:($\frac{1}{x-2}$-$\frac{1}{x+2}$)÷$\frac{4}{x-2}$(2)化简求值:(2a+b)2-2(a-2b)(2a+b),其中a,b分别为4的两个平方根(a>b).
分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果;
(2)原式利用完全平方公式,以及多项式乘以多项式法则计算,去括号合并得到最简结果,求出a与b的值,代入计算即可求出值.
解答 解:(1)原式=$\frac{x+2-x+2}{(x+2)(x-2)}$•$\frac{x-2}{4}$=$\frac{1}{x+2}$;
(2)原式=4a2+4ab+b2-2(2a2+ab-4ab-2b2)=4a2+4ab+b2-4a2-2ab+8ab+4b2=10ab+5b2,
∵a,b分别为4的两个平方根(a>b),∴a=2,b=-2,
当a=2,b=-2时,原式=-40+20=-20.
点评 此题考查了分式的混合运算,以及整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
9.已知x+y=8,xy=5,则x2+y2的值是( )
| A. | 84 | B. | 74 | C. | 64 | D. | 54 |
10.用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
| A. | 有一个内角小于90° | B. | 有一个内角小于或等于90° | ||
| C. | 每一个内角都小于90° | D. | 每一个内角都大于90° |
7.在一个直角三角形中,若其中两边长分别为5cm,3cm,则第三边长为( )
| A. | 4cm | B. | 4cm或$\sqrt{34}$cm | C. | $\sqrt{34}$cm | D. | 不存在 |
14.从图1到图2的变化过程可以发现的代数结论是( )
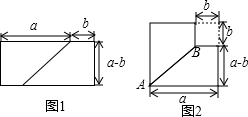

| A. | (a+b)(a-b)=a2-b2 | B. | a2-b2=(a+b)(a-b) | C. | (a+b)2=a2+2ab+b2 | D. | a2+2ab+b2=(a+b)2 |
9. 如图,不能判定AB∥DF的是( )
如图,不能判定AB∥DF的是( )
 如图,不能判定AB∥DF的是( )
如图,不能判定AB∥DF的是( )| A. | ∠1=∠2 | B. | ∠A=∠4 | C. | ∠1=∠A | D. | ∠A+∠3=180° |