题目内容
17.已知x2-4y2=20,x+2y=5,求x,y的值.分析 直接利用平方差公式分解因式,进而得出x-2y=4,再利用二元一次方程组的解法得出x,y的值.
解答 解:∵x2-4y2=(x+2y)(x-2y)=20,x+2y=5,
∴5(x-2y)=20,
∴x-2y=4,
∴$\left\{\begin{array}{l}{x+2y=5}\\{x-2y=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4.5}\\{y=0.25}\end{array}\right.$.
点评 此题主要考查了公式法分解因式以及二元一次方程组的解法,正确分解因式是解题关键.

练习册系列答案
相关题目
7.在一个直角三角形中,若其中两边长分别为5cm,3cm,则第三边长为( )
| A. | 4cm | B. | 4cm或$\sqrt{34}$cm | C. | $\sqrt{34}$cm | D. | 不存在 |
12.如果x2+kxy+9y2是一个完全平方式,那么k的值为( )
| A. | 6 | B. | -6 | C. | ±6 | D. | 18 |
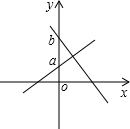
2.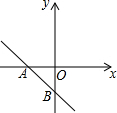 如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )
如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )
 如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )
如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )| A. | m>3 | B. | m<3 | C. | m>1 | D. | m<1 |
9. 如图,不能判定AB∥DF的是( )
如图,不能判定AB∥DF的是( )
 如图,不能判定AB∥DF的是( )
如图,不能判定AB∥DF的是( )| A. | ∠1=∠2 | B. | ∠A=∠4 | C. | ∠1=∠A | D. | ∠A+∠3=180° |
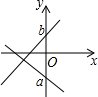
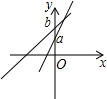
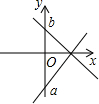
 如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=60°.
如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=60°.