题目内容
若抛物线经过点(3,0)和(2,-3),且以直线x=1为对称轴,则该抛物线的解析式为( )
A. y=-x2-2x-3 B. y=x2-2x+3
C. y=x2-2x-3 D. y=-x2+2x-3
 C
【解析】设抛物线的解析式为:y=ax²+bx+c,把(3,0)和(2,-3)代入抛物线解析式得: ,
由直线x=1为对称轴,得到,即b=-2a,
代入方程组得: ,
解得:a=1,b=-2,c=-3 ,
则抛物线解析式为y=x²-2x-3,
所以C选项是正确的
C
【解析】设抛物线的解析式为:y=ax²+bx+c,把(3,0)和(2,-3)代入抛物线解析式得: ,
由直线x=1为对称轴,得到,即b=-2a,
代入方程组得: ,
解得:a=1,b=-2,c=-3 ,
则抛物线解析式为y=x²-2x-3,
所以C选项是正确的
练习册系列答案
相关题目
已知 ,求
,求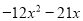 的值.
的值.
 -6
【解析】试题分析:
试题解析:
∵
∴
∴=-3×4x2-21x=-3(2-7x)-21x=-6+21x-21x=-6.
-6
【解析】试题分析:
试题解析:
∵
∴
∴=-3×4x2-21x=-3(2-7x)-21x=-6+21x-21x=-6. 二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ac>0;②2a+b=0;③a+b+c=0;④当x>1时,函数y随x的增大而增大;⑤当y>0时,-1<x<3.其中,正确的说法有___________(请写出所有正确说法的序号).
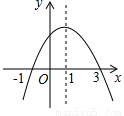
 ②⑤
【解析】试题解析::∵抛物线的开口向下,与y轴的交点在y轴的正半轴上,
∴a<0,c>0,
∴ac<0,∴①错误;
由图象可知:-=1,
∴2a+b=0,∴②正确;
当x=1时,y=a+b+c>0,∴③错误;
由图象可知:当x>1时,函数y随x的增大而减小,∴④错误;
根据图象,当-1<x<3时,y>0,∴⑤正确;
正确的说法有②⑤.
②⑤
【解析】试题解析::∵抛物线的开口向下,与y轴的交点在y轴的正半轴上,
∴a<0,c>0,
∴ac<0,∴①错误;
由图象可知:-=1,
∴2a+b=0,∴②正确;
当x=1时,y=a+b+c>0,∴③错误;
由图象可知:当x>1时,函数y随x的增大而减小,∴④错误;
根据图象,当-1<x<3时,y>0,∴⑤正确;
正确的说法有②⑤. 函数y=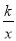 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A. 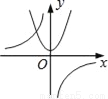 B.
B. 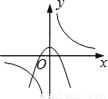 C.
C. 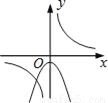 D.
D. 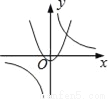
 B
【解析】A选项中,若反比例函数如图,则,那么抛物线应与y轴交于负半轴,所以A不可能;
B选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以B可能;
C选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以C不可能;
D选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以D不可能;
故选B.
...
B
【解析】A选项中,若反比例函数如图,则,那么抛物线应与y轴交于负半轴,所以A不可能;
B选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以B可能;
C选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以C不可能;
D选项中,若反比例函数如图,则,那抛物线开口应该向下,且与y轴交于正半轴,所以D不可能;
故选B.
... 抛物线y=ax2+bx+c的图象如图所示,则它关于y轴对称的抛物线的解析式是____.
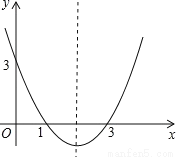
 y=x2+4x+3
【解析】∵点(1,0),(3,0),(0,3)关于y轴的对称点是(?1,0),(?3,0),(0,3).
则a?b+c=0,9a?3b+c=0,c=3联立方程组解得:a=1,b=4,c=3.
∴y=x²+4x+3;
方法二:由题意可知,抛物线y=x2+bx+c经过(1,0),(3,0),(0,3).
∴y=x²?4x+3.
∴关于y轴对称的抛...
y=x2+4x+3
【解析】∵点(1,0),(3,0),(0,3)关于y轴的对称点是(?1,0),(?3,0),(0,3).
则a?b+c=0,9a?3b+c=0,c=3联立方程组解得:a=1,b=4,c=3.
∴y=x²+4x+3;
方法二:由题意可知,抛物线y=x2+bx+c经过(1,0),(3,0),(0,3).
∴y=x²?4x+3.
∴关于y轴对称的抛... 已知二次函数的图象经过点(0,-1)、(1,-3)、(-1,3),求这个二次函数的解析式.
 【解析】分析:设二次函数的解析式为,再把(0,-1)、(1,-3)、(-1,3)分别代入得到关于a、b、c的方程组,解方程组求出a、b、c的值,从而得到二次函数的解析式.
本题解析:设二次函数的解析式为,
由题意得,
解得.
故二次函数的解析式为.
【解析】分析:设二次函数的解析式为,再把(0,-1)、(1,-3)、(-1,3)分别代入得到关于a、b、c的方程组,解方程组求出a、b、c的值,从而得到二次函数的解析式.
本题解析:设二次函数的解析式为,
由题意得,
解得.
故二次函数的解析式为. 关于抛物线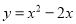 ,下列说法正确的是( )
,下列说法正确的是( )
A. 顶点是坐标原点
B. 对称轴是直线x=2
C. 有最高点
D. 经过坐标原点
 D
【解析】∵,
,
,
∴顶点坐标是:(1,-1),对称轴是直线x=1,
∵a=1>0,∴开口向上,
有最小值,
∵当x=0时, ,
∴图象经过坐标原点,
故选:D.
D
【解析】∵,
,
,
∴顶点坐标是:(1,-1),对称轴是直线x=1,
∵a=1>0,∴开口向上,
有最小值,
∵当x=0时, ,
∴图象经过坐标原点,
故选:D. 解下列分式方程.
(1) 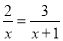 ; (2)
; (2) 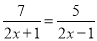 ;
;
(3) 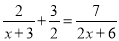 ; (4)
; (4) 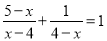 .
.
 (1) x=2.(2) x=3.(3) x=-2. (4)无解.
【解析】试题分析:每个方程确定最简公分母后,方程两边乘最简公分母,把分式方程转化为整式方程求解后再进行检验即可得.
试题解析:(1)方程两边同乘x(x+1),得
2(x+1)=3x,
解得:x=2,
检验:当x=2时,x(x+1)≠0,
所以原方程的解为x=2;
(2)方程两边同乘(2x-1...
(1) x=2.(2) x=3.(3) x=-2. (4)无解.
【解析】试题分析:每个方程确定最简公分母后,方程两边乘最简公分母,把分式方程转化为整式方程求解后再进行检验即可得.
试题解析:(1)方程两边同乘x(x+1),得
2(x+1)=3x,
解得:x=2,
检验:当x=2时,x(x+1)≠0,
所以原方程的解为x=2;
(2)方程两边同乘(2x-1... 一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为_________小时(用根号表示).
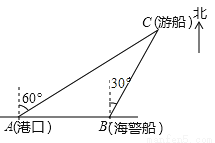
 【解析】试题分析:过点C作CD⊥AB,则在Rt△ACD中,AC=60海里,∠CAD=30°可得:CD=30海里;在Rt△CBD中,∠CBD=60°,则BC=20海里,则t=20÷40=小时.
【解析】试题分析:过点C作CD⊥AB,则在Rt△ACD中,AC=60海里,∠CAD=30°可得:CD=30海里;在Rt△CBD中,∠CBD=60°,则BC=20海里,则t=20÷40=小时. 
