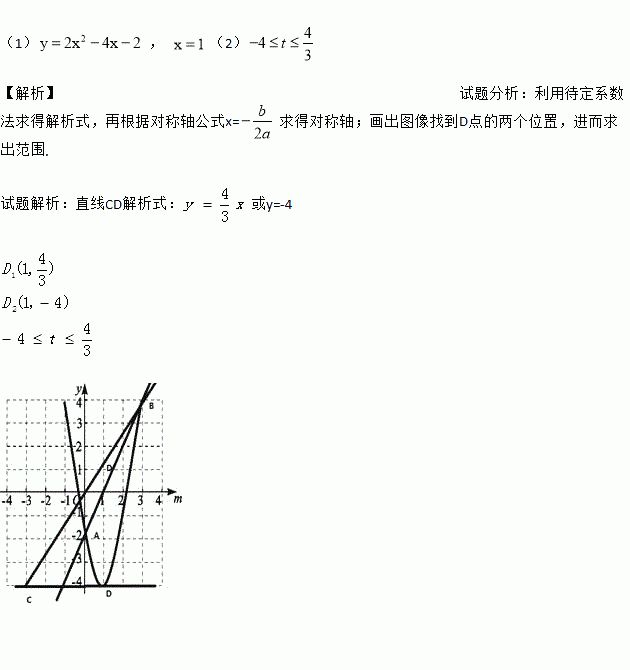��Ŀ����
��8�֣���ƽ��ֱ������ϵxOy�У�������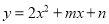 ������A��0��-2��,B��3��4����
������A��0��-2��,B��3��4����
��1���������ߵı���ʽ���Գ��
��2�����B����ԭ��ĶԳƵ�ΪC,��D�������߶Գ�����һ���㣬����������A,B֮��IJ���Ϊͼ��G������A,B���㣩.��ֱ��CD��ͼ��G�й����㣬��Ϻ���ͼ�����D������t ��ȡֵ��Χ��
 ��1���� ��2��
��������������������ô���ϵ������ý���ʽ���ٸ��ݶԳ��ṫʽx=��öԳ������ͼ���ҵ�D�������λ�ã����������Χ.
���������ֱ��CD����ʽ����y=-4
��1���� ��2��
��������������������ô���ϵ������ý���ʽ���ٸ��ݶԳ��ṫʽx=��öԳ������ͼ���ҵ�D�������λ�ã����������Χ.
���������ֱ��CD����ʽ����y=-4
 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д���m____ʱ������y��(m��2)x2��4x��5(m�dz���)�Ƕ��κ�����
 ��2
�����������ݶ��κ����ĸ����֪m-2��0�����m��2.
�ʴ�Ϊ����2.
��2
�����������ݶ��κ����ĸ����֪m-2��0�����m��2.
�ʴ�Ϊ����2. ���и�ʽ�����ҵı����У�����ʽ�ֽ���ǣ� ��.
A. x��a-b��=ax-bx B. x2-1+y2=��x-1����x+1��+y2
C. y2-1=��y+1����y-1�� D. ax+bx+c=x��a+b��+c
 C
��������A. ����ʽ�ij˷�����A����
B. û��һ������ʽת���ɼ�����ʽ������B����
C. ��һ������ʽת���ɼ�����ʽ������C��ȷ��
D. û��һ������ʽת���ɼ�����ʽ������D����
��ѡ��C.
C
��������A. ����ʽ�ij˷�����A����
B. û��һ������ʽת���ɼ�����ʽ������B����
C. ��һ������ʽת���ɼ�����ʽ������C��ȷ��
D. û��һ������ʽת���ɼ�����ʽ������D����
��ѡ��C. ������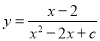 ���Ա���x��ȡֵ��Χ��ȫ��ʵ������c��ȡֵ��Χ�ǣ�������
���Ա���x��ȡֵ��Χ��ȫ��ʵ������c��ȡֵ��Χ�ǣ�������
A. c��1
B. c=1
C. c��1
D. c��1
 A
���������ȸ��ݷ�ʽ�����壬��ĸ������0���ó����ٸ��ݶ��κ�����a��0����ͼ�����ʣ���֪��������ϵ��a��0����=ʱ����y��0����ʱ�Ա���x��ȡֵ��Χ��ȫ��ʵ�������c��1��
��ѡ��A��
A
���������ȸ��ݷ�ʽ�����壬��ĸ������0���ó����ٸ��ݶ��κ�����a��0����ͼ�����ʣ���֪��������ϵ��a��0����=ʱ����y��0����ʱ�Ա���x��ȡֵ��Χ��ȫ��ʵ�������c��1��
��ѡ��A�� ��ͬһֱ������ϵ�У�����y=kx2��k��y=kx+k��k��0����ͼ������ǣ�������
A. 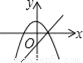 B.
B. 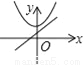 C.
C. 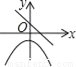 D.
D. 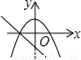
 D
����������������� A����һ�κ���y=kx+k��ͼ��ɵã�k��0����ʱ���κ���y=kx2��kx��ͼ��Ӧ�ÿ������ϣ�����
B����һ�κ���y=kx+kͼ���֪��k��0����ʱ���κ���y=kx2��kx��ͼ��Ӧ��y��ĸ����ᣬ����
C����һ�κ���y=kx+k��֪��y��x�������Сʱ��ֱ����y�ύ�ڸ����ᣬ����
D����ȷ��
��ѡ��D��
D
����������������� A����һ�κ���y=kx+k��ͼ��ɵã�k��0����ʱ���κ���y=kx2��kx��ͼ��Ӧ�ÿ������ϣ�����
B����һ�κ���y=kx+kͼ���֪��k��0����ʱ���κ���y=kx2��kx��ͼ��Ӧ��y��ĸ����ᣬ����
C����һ�κ���y=kx+k��֪��y��x�������Сʱ��ֱ����y�ύ�ڸ����ᣬ����
D����ȷ��
��ѡ��D�� ������y��ax2��bx��c��ͼ����ͼ��ʾ����������y��ԳƵ������ߵĽ���ʽ��____��
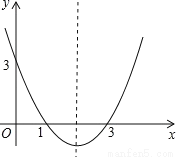
 y��x2��4x��3
���������ߵ�(1,0),(3,0),(0,3)����y��ĶԳƵ���(?1,0),(?3,0),(0,3).
��a?b+c=0��9a?3b+c=0��c=3�����������ã�a=1��b=4��c=3.
��y=x²+4x+3��
���������������֪,������y=x2+bx+c����(1,0),(3,0),(0,3).
��y=x²?4x+3.
�����y��ԳƵ���...
y��x2��4x��3
���������ߵ�(1,0),(3,0),(0,3)����y��ĶԳƵ���(?1,0),(?3,0),(0,3).
��a?b+c=0��9a?3b+c=0��c=3�����������ã�a=1��b=4��c=3.
��y=x²+4x+3��
���������������֪,������y=x2+bx+c����(1,0),(3,0),(0,3).
��y=x²?4x+3.
�����y��ԳƵ���... ��֪�����ߵĶ�������ΪP��2��-1��������ͼ����C��0��3����
��1����������ߵĽ���ʽ��
��2����������ߵ�ͼ����x�ύ��A��B���㣬���ABC�������
 ��1������2��3
����������������1����������߷���Ϊ ��Ȼ�㣨3��0���������k��ֵ����2����y=0�������������x��Ľ������꣬Ȼ����������ε������ʽ��ʽ������⣮
�����������1���������ߵĶ�������ΪP��2��-1����
����������߷���Ϊ����k��0����
������ͼ����C��0��3����
�࣬
���k=1��
��������ߵĽ���ʽΪ������
��2����...
��1������2��3
����������������1����������߷���Ϊ ��Ȼ�㣨3��0���������k��ֵ����2����y=0�������������x��Ľ������꣬Ȼ����������ε������ʽ��ʽ������⣮
�����������1���������ߵĶ�������ΪP��2��-1����
����������߷���Ϊ����k��0����
������ͼ����C��0��3����
�࣬
���k=1��
��������ߵĽ���ʽΪ������
��2����... ���κ���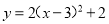 �Ķ�����ϵ����һ����ϵ����������ֱ�Ϊ��������
�Ķ�����ϵ����һ����ϵ����������ֱ�Ϊ��������
A. 2��12��20
B. 2x2��-12��20
C. 2��-12��20
D. 2��-12x��20
 C
���������ߣ�
�������ϵ��Ϊ2��һ����ϵ��Ϊ-12��������Ϊ20��
��ѡ��C��
C
���������ߣ�
�������ϵ��Ϊ2��һ����ϵ��Ϊ-12��������Ϊ20��
��ѡ��C�� ƽʱ����������ʱ����ҡ����ߵ㴦����״�ɽ��Ƶؿ��������ߣ���ͼ��ʾ������ҡ���ļס�������ͬѧ�������ּ��Ϊ4 m����ظ߾�Ϊ1 m��ѧ���������ֱ�վ�ھ����������ˮƽ����1 m��2��5 m����������ҡ����ߴ�ʱ�պ�ͨ�����ǵ�ͷ������֪ѧ������������1��5 m����ѧ����������Ϊ ( )
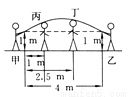
A. 1.5 m B. 1.625 m C. 1.66 m D. 1.67 m
 B
��������������ĺ����Ľ���ʽΪy=ax2+bx+c������֪��������ͼ�����-1��1������0��1.5������3��1�����㣬���������ʽΪy=-x2+x+,�߶�ͷ���ĺ�����Ϊ1.5������������ʽ�������������Ϊ1.625m.��ѡB.
B
��������������ĺ����Ľ���ʽΪy=ax2+bx+c������֪��������ͼ�����-1��1������0��1.5������3��1�����㣬���������ʽΪy=-x2+x+,�߶�ͷ���ĺ�����Ϊ1.5������������ʽ�������������Ϊ1.625m.��ѡB.