题目内容
14.观察下列等式:①$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}-1$;
②$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}-\sqrt{2}$;
③$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\sqrt{4}$-$\sqrt{3}$;…
回答下列问题:
(1)化简:$\frac{1}{\sqrt{2015}+\sqrt{2014}}$=$\sqrt{2015}$-$\sqrt{2014}$;
(2)化简:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;(n为正整数);
(3)利用上面所揭示的规律计算:
$\frac{1}{1+\sqrt{2}}$$+\frac{1}{\sqrt{2}+\sqrt{3}}$$+\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2014}}$+$\frac{1}{\sqrt{2014}+\sqrt{2015}}$.
分析 (1)根据已知得出式子变化规律写出答案即可;
(2)进而由(1)的规律得出答案;
(3)利用发现的规律化简各式进而求出即可.
解答 解:(1)$\frac{1}{\sqrt{2015}+\sqrt{2014}}$=$\sqrt{2015}$-$\sqrt{2014}$;
故答案为:$\sqrt{2015}$-$\sqrt{2014}$;
(2)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;(n为正整数);
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(3)$\frac{1}{1+\sqrt{2}}$$+\frac{1}{\sqrt{2}+\sqrt{3}}$$+\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2014}}$+$\frac{1}{\sqrt{2014}+\sqrt{2015}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2014}$-$\sqrt{2013}$+$\sqrt{2015}$-$\sqrt{2014}$
=$\sqrt{2015}$-1.
点评 此题主要考查了分母有理化,正确发现式子中变化规律是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
2.我市某游乐场在暑假期间推出学生个人门票优惠活动,各类门票价格如下表:
某慈善单位欲购买三种类型的门票共100张奖励品学兼优的留守学生,设购买A种票x张,B种票张数是A种票的3倍还多7张,C种票y张,根据以上信息解答下列问题:
(1)直接写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买学生的夜场票不低于20张,且节假日通票至少购买5张,有哪几种购票方案?哪种方案费用最少?
| 票价种类 | (A)夜场票 | (B)日通票 | (C)节假日通票 |
| 单价(元) | 80 | 120 | 150 |
(1)直接写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买学生的夜场票不低于20张,且节假日通票至少购买5张,有哪几种购票方案?哪种方案费用最少?
9.已知点P是线段AB的一个黄金分割点(AP>PB),则PB:AB的值为( )
| A. | $\frac{3-\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\frac{3-\sqrt{5}}{4}$ |
19.若x-y=2,x-z=3,则(y-z)2-3(z-y)+9的值为( )
| A. | 13 | B. | 11 | C. | 5 | D. | 7 |
6.生物兴趣小组在同一温箱里培育甲、乙两种菌种,如果甲菌种生长温度x℃的范围是34≤x≤37,乙菌种生长温度y℃的范围是33≤y≤35.那么温箱里应设置温度T℃的范围是( )
| A. | 34≤T≤37 | B. | 34≤T≤35 | C. | 33≤T≤35 | D. | 35≤T≤37 |
4.云南地区地震发生后,全国人民抗旱救灾,众志成城.温州市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,温州市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
(2)为了节省运费,温州市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
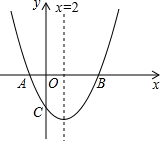 如图,经过点C(0,-4)的抛物线y=ax2+bx+c(a≠0)与x轴相交于A(-2,0),B两点.
如图,经过点C(0,-4)的抛物线y=ax2+bx+c(a≠0)与x轴相交于A(-2,0),B两点. 如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.
如图,AB为半圆O的直径,M为半圆内的一点,直线AM交半圆O于点C,直线BM交半圆O于点D,直线DC与直线AB交于点P,N为直径AB上的一点,且满足ON•OP=OB2,求证:MN⊥AB.