题目内容
3.已知x1、x2是关于x的方程x2-px+q=0的两根,且$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=3,x12+x22=7.求:p+q的值.分析 根据一元二次方程根与系数的关系得到x1+x2=p,x1•x2=q,则x12+x22=(x1+x2)2-2x1•x2=p2-2q=7,即p2-2q=7,①$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{p}{q}$=3,即$\frac{p}{q}$=3,②由①②联立可以求得p、q的值.
解答 解:∵关于x的方程x2-px+q=0的两根分别是x1、x2,
∴x1+x2=p,x1•x2=q,
∴x12+x22=(x1+x2)2-2x1•x2=p2-2q=7,即p2-2q=7,①$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$═$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{p}{q}$=3,即$\frac{p}{q}$=3,②
由①②,得9q2-2q-7=0,
(q-1)(9q+7)=0,
解得,q=1,p=3或q=-$\frac{7}{9}$,p=-$\frac{7}{3}$;
∴p+q=3+1=4或p+q=-$\frac{7}{9}$-$\frac{7}{9}$=-$\frac{28}{9}$,
综上所述,p+q的值是4或-$\frac{28}{9}$.
点评 此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.若反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象过点(3,-4),则下列各点中也在该图象上的点是( )
| A. | (2,6) | B. | (-6,-2) | C. | (-3,4) | D. | (-3,-4) |
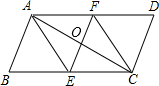 如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.
如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.