题目内容
2.我市某游乐场在暑假期间推出学生个人门票优惠活动,各类门票价格如下表:| 票价种类 | (A)夜场票 | (B)日通票 | (C)节假日通票 |
| 单价(元) | 80 | 120 | 150 |
(1)直接写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买学生的夜场票不低于20张,且节假日通票至少购买5张,有哪几种购票方案?哪种方案费用最少?
分析 (1)根据总票数为100得到x+3x+7+y=100,然后用x表示y即可;
(2)利用表中数据把三种票的费用加起来得到w=80x+120(3x+7)+150(93-4x),然后整理即可;
(3)根据题意得到不等式组,再解不等式组且确定不等式组的整数解为20、21、22,于是得到共有3种购票方案,然后根据一次函数的性质求w的最小值.
解答 解:(1)根据题意,
x+3x+7+y=100,
所以y=93-4x;
(2)w=80x+120(3x+7)+150(93-4x)=-160x+14790;
(3)依题意得$\left\{\begin{array}{l}{x≥20}\\{93-4x≥5}\\{3x+7≥5}\end{array}\right.$
解得20≤x≤22,
因为整数x为20、21、22,
所以共有3种购票方案(A、20,B、67,C、13;A、21,B、70,C、9;A、22,B、73,C、5);
而w=-160x+14790,
因为k=-160<0,
所以y随x的增大而减小,
所以当x=22时,y最小=22×(-160)+14790=11270,
即当A种票为22张,B种票73张,C种票为5张时费用最少,最少费用为11270元.
点评 本题考查了一次函数的运用,读懂题意列出函数表达式以及一元一次不等式组,运用一次函数的性质解决最值问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.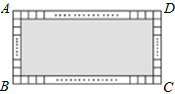 如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
 如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )| A. | 5:3 | B. | 11:7 | C. | 23:15 | D. | 47:29 |
7.已知3x=4y,则$\frac{x}{y}$的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{7}$ |
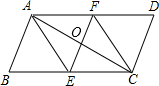 如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.
如图,在?ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,分别交BC,AD于点E,F,连接AC,EF相交于点O.若点E是BC的中点,AB⊥AC,AB=2,则四边形AECF的面积是2$\sqrt{3}$.