题目内容
9.已知点P是线段AB的一个黄金分割点(AP>PB),则PB:AB的值为( )| A. | $\frac{3-\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\frac{3-\sqrt{5}}{4}$ |
分析 把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比.
解答 解:根据题意得AP=$\frac{\sqrt{5}-1}{2}$AB,
所以PB=AB-AP=$\frac{3-\sqrt{5}}{2}$AB,
所以PB:AB=$\frac{3-\sqrt{5}}{2}$.
故选A.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点;其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.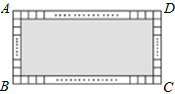 如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
 如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )
如图,将矩形ABCD分割成1个灰色矩形与148个面积相等的小正方形,若灰色矩形之长与宽的比为5:3,则AD:AB的值是( )| A. | 5:3 | B. | 11:7 | C. | 23:15 | D. | 47:29 |
1.有六张不透明的卡片,正面的数分别为3.1,$\frac{7}{3}$,$\sqrt{\frac{1}{4}}$,π,$\sqrt{6}$,3.$\stackrel{••}{12}$,除正面的数不同外,其余都相同,将它们背面朝上洗匀后,从中随机抽取一张卡片,抽到写有无理数卡片的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |