题目内容
11.设a,b,c分别是△ABC的边长,若∠B=2∠A,则下列关系是成立的是( )| A. | $\frac{a}{b}$$>\frac{a+b}{a+b+c}$ | B. | $\frac{a}{b}$$<\frac{a+b}{a+b+c}$ | C. | $\frac{a}{b}$=$\frac{a+b}{a+b+c}$ | D. | 无法确定 |
分析 延长CB至D,使BD=AB,于是得到CD=a+c,根据等腰三角形的性质得到∠BAD=∠D,根据三角形的外角的性质得到∠ABC=∠BAD+∠D,证得∠BAC=∠D,由于∠C=∠C,推出△ABC∽△DAC,根据相似三角形的性质得到$\frac{AC}{CD}=\frac{BC}{AC}$,即$\frac{b}{a+c}=\frac{a}{b}$,根据合比的性质即可得到$\frac{a+b}{a+b+c}=\frac{a}{b}$.
解答 解:延长CB至D,使BD=AB,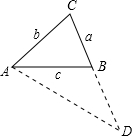
于是CD=a+c,∠BAD=∠D,
∵∠ABC=∠BAD+∠D,
∴∠ABC=2∠D,
∵∠ABC=2∠BAC,
∴∠BAC=∠D,
∵∠C=∠C
∴△ABC∽△DAC,
∴$\frac{AC}{CD}=\frac{BC}{AC}$,即:$\frac{b}{a+c}=\frac{a}{b}$,
∴$\frac{a+b}{a+b+c}=\frac{a}{b}$,
故选C.
点评 本题考查了三角形的边角关系,相似三角形对应边比值相等的性质,比例的性质,相似三角形的判定,本题中求证△ABC∽△DAC是解题的关键.

练习册系列答案
相关题目
3.计算4m•8-1÷2m的值为512,则m的值等于( )
| A. | 12 | B. | 3 | C. | 5 | D. | 4 |
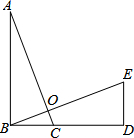 如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°.
如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°.