题目内容
7.若式子$\frac{\sqrt{2x-5}}{3}$在实数范围内有意义,则x的取值范围是( )| A. | x>$\frac{5}{2}$ | B. | x≥-$\frac{5}{2}$ | C. | x≥$\frac{5}{2}$ | D. | x≥-$\frac{5}{2}$且x≠0 |
分析 首先根据二次根式有意义的条件,可得2x-5≥0;然后根据一元一次不等式的解法,求出x的取值范围是多少即可.
解答 解:∵式子$\frac{\sqrt{2x-5}}{3}$在实数范围内有意义,
∴2x-5≥0,
∴x≥$\frac{5}{2}$,
即x的取值范围是x≥$\frac{5}{2}$.
故选:C.
点评 (1)此题主要考查了二次根式有意义的条件,要熟练掌握,解答此题的关键是要明确:(1)如果一个式子中含有多个二次根式,那么它们有意义的条件是:各个二次根式中的被开方数都必须是非负数.(2)如果所给式子中含有分母,则除了保证被开方数为非负数外,还必须保证分母不为零.
(2)此题还考查了一元一次不等式的解法,要熟练掌握.

练习册系列答案
相关题目
17.若一个正六边形的半径为2,则它的边心距等于( )
| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
15.学习了一次函数、二次函数、反比例函数后,爱钻研的小敏尝试用同样的方法研究函数y=$\frac{3x+1}{x}$,从而得出以下命题:
(1)当x>0时,y的值随着x的增大而减小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近3;
(4)当y>0时,x>0或x<-$\frac{1}{3}$.
你认为真命题是( )
(1)当x>0时,y的值随着x的增大而减小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近3;
(4)当y>0时,x>0或x<-$\frac{1}{3}$.
你认为真命题是( )
| A. | (1)(3) | B. | (1)(4) | C. | (1)(3)(4) | D. | (2)(3)(4) |
12.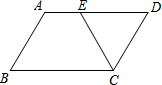 ?ABCD中,CE平分∠BCD.若BC=10,AE=4,则?ABCD的周长是( )
?ABCD中,CE平分∠BCD.若BC=10,AE=4,则?ABCD的周长是( )
 ?ABCD中,CE平分∠BCD.若BC=10,AE=4,则?ABCD的周长是( )
?ABCD中,CE平分∠BCD.若BC=10,AE=4,则?ABCD的周长是( )| A. | 28 | B. | 32 | C. | 36 | D. | 40 |