题目内容
18.如图,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,连接BE和CG. 求证:四边形BGCE是平行四边形.
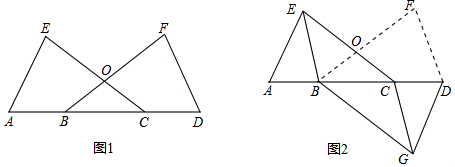
分析 (1)直接利用等腰三角形的性质结合全等三角形的判定与性质得出即可;
(2)利用翻折变换的性质得出∠DBG=∠DBF,再利用平行线的判定方法得出CE∥BG,进而求出四边形BGCE是平行四边形.
解答 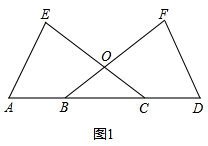 证明:(1)如图1,
证明:(1)如图1,
∵OB=OC,
∴∠ACE=∠DBF,
在△ACE和△DBF中,
$\left\{\begin{array}{l}{∠ACE=∠DBF}\\{∠E=∠F}\\{AE=FD}\end{array}\right.$,
∴△ACE≌△DBF(AAS);
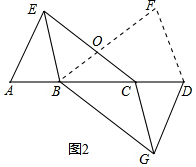
(2)如图2,
∵∠ACE=∠DBF,∠DBG=∠DBF,
∴∠ACE=∠DBG,
∴CE∥BG,
∵CE=BF,BG=BF,
∴CE=BG,
∴四边形BGCE是平行四边形.
点评 此题主要考查了全等三角形的判定与性质以及平行四边形的判定等知识,得出CE∥BG是解题关键.

练习册系列答案
相关题目
6.一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
(公式:方差s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overrightarrow{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$是平均数.)
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=$\frac{个人成绩-平均成绩}{标准差}$.(说明:标准差为方差的算术平方根)
从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
| A | B | C | D | E | 平均分 | 方差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | 70 | 2 |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 | 36 |
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=$\frac{个人成绩-平均成绩}{标准差}$.(说明:标准差为方差的算术平方根)
从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
3. 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,若把直角三角形绕边AB所在直线旋转一周,则所得几何体的表面积为( )
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,若把直角三角形绕边AB所在直线旋转一周,则所得几何体的表面积为( )
 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,若把直角三角形绕边AB所在直线旋转一周,则所得几何体的表面积为( )
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,若把直角三角形绕边AB所在直线旋转一周,则所得几何体的表面积为( )| A. | $\frac{84}{5}$π | B. | $\frac{168}{5}$π | C. | 12π | D. | 24π |
7.若式子$\frac{\sqrt{2x-5}}{3}$在实数范围内有意义,则x的取值范围是( )
| A. | x>$\frac{5}{2}$ | B. | x≥-$\frac{5}{2}$ | C. | x≥$\frac{5}{2}$ | D. | x≥-$\frac{5}{2}$且x≠0 |
8.甲、乙两商场各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题意,填写下表(单位:元):
(2)当x取何值时,小红在甲、乙两商场的实际花费金额相同?
(3)请你根据小红累计购物的金额选择花费较少的商场?
(1)根据题意,填写下表(单位:元):
| 累计购物金额 实际花费金额 | 130 | 290 | … | x |
| 甲商场 | 127 | 271 | … | 0.9x+10 |
| 乙商场 | 126 | 278 | … | 0.95x+2.5 |
(3)请你根据小红累计购物的金额选择花费较少的商场?
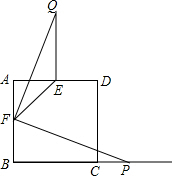 如图,正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FQ,连接EQ,则EF、EQ、BP三者之间的数量关系为EF=$\sqrt{2}$(BP-EQ)..
如图,正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FQ,连接EQ,则EF、EQ、BP三者之间的数量关系为EF=$\sqrt{2}$(BP-EQ)..