题目内容
17.关于x的一元二次方程x2-x+p-1=0有两个实数根x1,x2,则p的取值范围是p$≤\frac{5}{4}$.分析 根据方程有实数根,得出△≥0,建立关于p的不等式,求出p的取值范围即可.
解答 解:由题意知,△=1-4p+4≥0,
∴p≤$\frac{5}{4}$,
故答案为p$≤\frac{5}{4}$.
点评 此题考查了根的判别式,掌握一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根是本题的关键.

练习册系列答案
相关题目
7.若式子$\frac{\sqrt{2x-5}}{3}$在实数范围内有意义,则x的取值范围是( )
| A. | x>$\frac{5}{2}$ | B. | x≥-$\frac{5}{2}$ | C. | x≥$\frac{5}{2}$ | D. | x≥-$\frac{5}{2}$且x≠0 |
8.甲、乙两商场各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题意,填写下表(单位:元):
(2)当x取何值时,小红在甲、乙两商场的实际花费金额相同?
(3)请你根据小红累计购物的金额选择花费较少的商场?
(1)根据题意,填写下表(单位:元):
| 累计购物金额 实际花费金额 | 130 | 290 | … | x |
| 甲商场 | 127 | 271 | … | 0.9x+10 |
| 乙商场 | 126 | 278 | … | 0.95x+2.5 |
(3)请你根据小红累计购物的金额选择花费较少的商场?
5.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在规定时间内每人踢100个以上(含100个)为优秀,下表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)
统计发现两班总数相等,此时有人建议,可以通过考查数据中的其他信息来评判.试从两班比赛数据的中位数、方差、优秀率三个方面考虑,你认为应该选定哪一个班为冠军?
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 96 | 110 | 90 | 104 | 500 |
2.某校准备修建一个面积为180平方米的矩形活动场地,它的长比宽多11米,设场地的宽为x米,则可列方程为( )
| A. | x(x-11)=180 | B. | 2x+2(x-11)=180 | C. | x(x+11)=180 | D. | 2x+2(x+11)=180 |
9.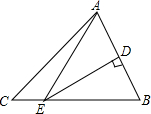 如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
 如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
6.经过某十字路口的汽车,可能直行,也可能左转或者右转,如果这三种可能性大小相同,则经过这个十字路口的两辆汽车一辆左转,一辆右转的概率是( )
| A. | $\frac{4}{7}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
3.下列各式中,计算正确的是( )
| A. | (3x-y)(3x-y)=9x2-y2 | B. | (-x+y)(-x-y)=x2-y2 | C. | (x+9)(x-9)=x2-9 | D. | (x-1)2=x2-2x-1 |
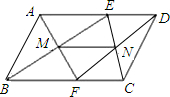 已知如图,在?ABCD中,E、F分别是AD、BC的中点,求证:MN∥BC,且MN=$\frac{1}{2}$BC.
已知如图,在?ABCD中,E、F分别是AD、BC的中点,求证:MN∥BC,且MN=$\frac{1}{2}$BC.