题目内容
17.若一个正六边形的半径为2,则它的边心距等于( )| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 根据正六边形的边长与外接圆的半径相等,构建直角三角形,利用直角三角形的边角关系即可求出.
解答  解:已知正六边形的半径为2,则正六边形ABCDEF的外接圆半径为2,
解:已知正六边形的半径为2,则正六边形ABCDEF的外接圆半径为2,
连接OA,作OM⊥AB于点M,
得到∠AOM=30°,
则OM=OA•cos30°=$\sqrt{3}$.
则正六边形的边心距是$\sqrt{3}$.
故选C.
点评 此题主要考查了正六边形和圆,利用连接正六边形的中心与各个顶点,正六边形被半径分成六个全等的正三角形得出是解题关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
6.一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
(公式:方差s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overrightarrow{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$是平均数.)
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=$\frac{个人成绩-平均成绩}{标准差}$.(说明:标准差为方差的算术平方根)
从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
| A | B | C | D | E | 平均分 | 方差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | 70 | 2 |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 | 36 |
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=$\frac{个人成绩-平均成绩}{标准差}$.(说明:标准差为方差的算术平方根)
从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
7.若式子$\frac{\sqrt{2x-5}}{3}$在实数范围内有意义,则x的取值范围是( )
| A. | x>$\frac{5}{2}$ | B. | x≥-$\frac{5}{2}$ | C. | x≥$\frac{5}{2}$ | D. | x≥-$\frac{5}{2}$且x≠0 |
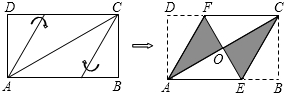
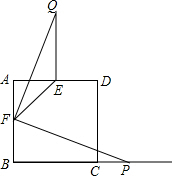 如图,正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FQ,连接EQ,则EF、EQ、BP三者之间的数量关系为EF=$\sqrt{2}$(BP-EQ)..
如图,正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FQ,连接EQ,则EF、EQ、BP三者之间的数量关系为EF=$\sqrt{2}$(BP-EQ)..