题目内容
方程(x-1)2+(y-1)2=xy+7的所有正整数解有( )组.
| A、1 | B、2 | C、3 | D、4 |
考点:非一次不定方程(组)
专题:
分析:根据x、y的对称性,可以分别给出x的正整数值,求得y的值,即可判断.
解答:解:∵(x-1)2+(y-1)2=xy+7,
∴(x-1)2+(y-1)2-xy-7=0,
∵0=(x-1)2+(y-1)2-xy-7≥2(x-1)(y-1)-xy-7,
∴2(x-1)(y-1)-xy-7≤0,
即(x-2)(y-2)≤9.
当x=1时,代入(x-1)2+(y-1)2=xy+7得:(y-1)2=y+7,此时y不是整数.
同理,当y=1时,x不是整数;
当x=2时,把x=2代入(x-1)2+(y-1)2=xy+7得,1+(y-1)2=2y+7,解得:y=5或-1(舍去),
则方程有正整数解:
,
同理,有正整数解
;
当x=3时,代入(x-1)2+(y-1)2=xy+7得:4+(y-1)2=3y+7,解得:y=
(舍去);
同理,当y=3时,也没有正整数解;
当x=4时,代入(x-1)2+(y-1)2=xy+7得:9+(y-1)2=4y+7,解得:y=3±
,
同理,当y=4时,也没有正整数解;
当x=5时,代入(x-1)2+(y-1)2=xy+7得:16+(y-1)2=5y+7,解得:y=5或2.
则方程有正整数解
,
.
同理,当y=5时,有整数解:
和
;
当x≥6时,y一定有y≥6,则(x-2)(y-2)≤9不成立,此时方程无解.
则方程的正整数解是:
,
,
共有3组.
故选C.
∴(x-1)2+(y-1)2-xy-7=0,
∵0=(x-1)2+(y-1)2-xy-7≥2(x-1)(y-1)-xy-7,
∴2(x-1)(y-1)-xy-7≤0,
即(x-2)(y-2)≤9.
当x=1时,代入(x-1)2+(y-1)2=xy+7得:(y-1)2=y+7,此时y不是整数.
同理,当y=1时,x不是整数;
当x=2时,把x=2代入(x-1)2+(y-1)2=xy+7得,1+(y-1)2=2y+7,解得:y=5或-1(舍去),
则方程有正整数解:
|
同理,有正整数解
|
当x=3时,代入(x-1)2+(y-1)2=xy+7得:4+(y-1)2=3y+7,解得:y=
5±
| ||
| 2 |
同理,当y=3时,也没有正整数解;
当x=4时,代入(x-1)2+(y-1)2=xy+7得:9+(y-1)2=4y+7,解得:y=3±
| 6 |
同理,当y=4时,也没有正整数解;
当x=5时,代入(x-1)2+(y-1)2=xy+7得:16+(y-1)2=5y+7,解得:y=5或2.
则方程有正整数解
|
|
同理,当y=5时,有整数解:
|
|
当x≥6时,y一定有y≥6,则(x-2)(y-2)≤9不成立,此时方程无解.
则方程的正整数解是:
|
|
|
故选C.
点评:本题考查了方程的正整数解,理解x、y的关系:让x=a时,求得y的值,与当y=a时,求得x的值,则x和值和y的值是相等的,理解这一性质是关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,若∠B=40°,∠EAD=16°,则∠C的度数是( )
如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,若∠B=40°,∠EAD=16°,则∠C的度数是( )| A、74° | B、72° |
| C、70° | D、68° |
 如图,在y轴上找一点C,使△ABC是等腰三角形,这样的C点共有( )个.
如图,在y轴上找一点C,使△ABC是等腰三角形,这样的C点共有( )个.| A、4 | B、3 | C、2 | D、1 |
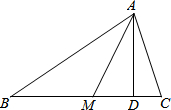 如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线.
如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线.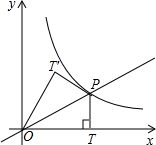 如图,点P(m,1)是双曲线y=
如图,点P(m,1)是双曲线y= 如图,已知,AC∥BD,CP⊥EP,点E在BD上,∠ACP=60°.
如图,已知,AC∥BD,CP⊥EP,点E在BD上,∠ACP=60°.