题目内容
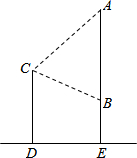
 如图,已知,AC∥BD,CP⊥EP,点E在BD上,∠ACP=60°.
如图,已知,AC∥BD,CP⊥EP,点E在BD上,∠ACP=60°.(1)点P是AB上一点,求∠PEB的度数;
(2)点P是AB外一点,∠CAB的角平分线与∠PED的角平分线交于点O,∠ABD度数为x,∠AOE度数为y.
①直接写出∠PEB的度数;
②用含x的式子表示y.
考点:三角形内角和定理,平行线的性质,三角形的外角性质
专题:
分析:(1)过P作PF∥AC,则PF∥AC∥BD,根据两直线平行内错角相等即可∠CPF=∠ACP=60°,∠PEB=∠EPF,因为CP⊥EP,∠PEB=∠EPF=30°,
(2)①同理可证∠PEB=30°,②由∠PEB=30°,即可求得∠PEO=75°因为∠CPE=90°,根据四边形的内角和为360°,即可求得用x表示y的式子.
(2)①同理可证∠PEB=30°,②由∠PEB=30°,即可求得∠PEO=75°因为∠CPE=90°,根据四边形的内角和为360°,即可求得用x表示y的式子.
解答:解:(1)过P作PF∥AC,
则PF∥AC∥BD,
∴∠CPF=∠ACP=60°,
∵CP⊥EP,
∴∠EPF=30°,
∴∠PEB=∠EPF=30°,
(2)①∠PEB=30°,
②∵AC∥BD,
∴∠BAC+∠ABD=180°
∵∠PEB=30°,
∴∠PED=150°,
∴∠PEO=75°,
∵∠CPE=90°,
∴∠AOE+(180°-∠ACP-
∠BAC)=195°,
∴y+[180°-60°-
(180°-x)=195°,
即y=165°-
x.
则PF∥AC∥BD,
∴∠CPF=∠ACP=60°,
∵CP⊥EP,
∴∠EPF=30°,
∴∠PEB=∠EPF=30°,
(2)①∠PEB=30°,
②∵AC∥BD,
∴∠BAC+∠ABD=180°
∵∠PEB=30°,
∴∠PED=150°,
∴∠PEO=75°,
∵∠CPE=90°,
∴∠AOE+(180°-∠ACP-
| 1 |
| 2 |
∴y+[180°-60°-
| 1 |
| 2 |
即y=165°-
| 1 |
| 2 |
点评:本题考查了平行线的性质,三角形的内角和定理,四边形内角和定理,熟练掌握性质和定理是本题的关键.

练习册系列答案
相关题目
方程(x-1)2+(y-1)2=xy+7的所有正整数解有( )组.
| A、1 | B、2 | C、3 | D、4 |
 如图所示,小明站在地面上照镜子,镜子AB挂在和地面垂直的墙面AE上,镜子的高度AB为(1+
如图所示,小明站在地面上照镜子,镜子AB挂在和地面垂直的墙面AE上,镜子的高度AB为(1+



 如图,AD∥BC,AD=BC,AE=CF.求证:
如图,AD∥BC,AD=BC,AE=CF.求证: 如图,△ABC的高BD、CE相交于点H,现给出四个判断:
如图,△ABC的高BD、CE相交于点H,现给出四个判断: