题目内容
 如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,若∠B=40°,∠EAD=16°,则∠C的度数是( )
如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,若∠B=40°,∠EAD=16°,则∠C的度数是( )| A、74° | B、72° |
| C、70° | D、68° |
考点:三角形内角和定理,三角形的角平分线、中线和高
专题:
分析:先根据AE⊥BC,∠EAD=16°求出∠ADE的度数,由三角形外角的性质求出∠BAD的度数,再根据AD平分∠BAC得出∠BAC的度数,根据三角形内角和定理即可得出结论.
解答:解:∵AE⊥BC,∠EAD=16°,
∴∠ADE=90°-16°=74°.
∵∠ADE是△ABD的外角,∠B=40°,
∴∠BAD=∠ADE-∠B=74°-40°=34°.
∵AD平分∠BAC得出∠BAC,
∴∠BAC=2∠BAD=2×34°=68°,
∴∠C=180°-∠BAC-∠B=180°-68°-40°=72°.
故选B.
∴∠ADE=90°-16°=74°.
∵∠ADE是△ABD的外角,∠B=40°,
∴∠BAD=∠ADE-∠B=74°-40°=34°.
∵AD平分∠BAC得出∠BAC,
∴∠BAC=2∠BAD=2×34°=68°,
∴∠C=180°-∠BAC-∠B=180°-68°-40°=72°.
故选B.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
方程(x-1)2+(y-1)2=xy+7的所有正整数解有( )组.
| A、1 | B、2 | C、3 | D、4 |
下列各组数中互为相反数的是( )
A、-2与
| |||
B、-2与
| |||
C、-2与-
| |||
| D、2与|-2| |
 如图,△ABC∽△ADE,AB=
如图,△ABC∽△ADE,AB=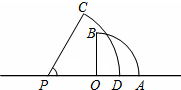 如图,以数轴上的原点O为圆心,6为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,10为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如果两个扇形的圆弧部分(
如图,以数轴上的原点O为圆心,6为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,10为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如果两个扇形的圆弧部分(




 如图,AD∥BC,AD=BC,AE=CF.求证:
如图,AD∥BC,AD=BC,AE=CF.求证: