题目内容
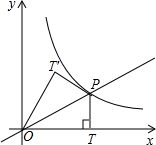 如图,点P(m,1)是双曲线y=
如图,点P(m,1)是双曲线y=
| ||
| x |
考点:翻折变换(折叠问题),反比例函数图象上点的坐标特征
专题:
分析:根据翻折变换的性质得出△T′OT是等边三角形,进而利用锐角三角形函数关系求出即可.
解答: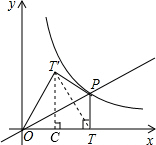 解:连接TT′,过点T′作T′C⊥OT于点C,
解:连接TT′,过点T′作T′C⊥OT于点C,
∵点P(m,1)是双曲线y=
上一点,
∴m=
,
则OT=
,PT=1,
故tan∠POT=
=
,
则∠POT=30°,
∵把△PTO沿直线OP翻折得到△PT′O,
∴∠T′OP=30°,OT=OT′,
∴△T′OT是等边三角形,
∴OC=CT=
,
T′C=OT′sin60°=
,
故T′的坐标为:(
,
).
故答案为:(
,
).
 解:连接TT′,过点T′作T′C⊥OT于点C,
解:连接TT′,过点T′作T′C⊥OT于点C,∵点P(m,1)是双曲线y=
| ||
| x |
∴m=
| 3 |
则OT=
| 3 |
故tan∠POT=
| 1 | ||
|
| ||
| 3 |
则∠POT=30°,
∵把△PTO沿直线OP翻折得到△PT′O,
∴∠T′OP=30°,OT=OT′,
∴△T′OT是等边三角形,
∴OC=CT=
| ||
| 2 |
T′C=OT′sin60°=
| 3 |
| 2 |
故T′的坐标为:(
| ||
| 2 |
| 3 |
| 2 |
故答案为:(
| ||
| 2 |
| 3 |
| 2 |
点评:此题主要考查了翻折变换的性质以及锐角三角函数关系等知识,得出△T′OT是等边三角形是解题关键.

练习册系列答案
相关题目
方程(x-1)2+(y-1)2=xy+7的所有正整数解有( )组.
| A、1 | B、2 | C、3 | D、4 |
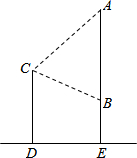 如图所示,小明站在地面上照镜子,镜子AB挂在和地面垂直的墙面AE上,镜子的高度AB为(1+
如图所示,小明站在地面上照镜子,镜子AB挂在和地面垂直的墙面AE上,镜子的高度AB为(1+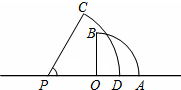 如图,以数轴上的原点O为圆心,6为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,10为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如果两个扇形的圆弧部分(
如图,以数轴上的原点O为圆心,6为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,10为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如果两个扇形的圆弧部分(
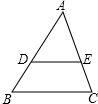 如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC=
如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC=


