题目内容
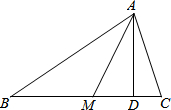 如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线.
如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线.(1)若∠BAD=50°,求高线AD与角平分线AM的夹角∠MAD的度数.
(2)若∠MAD=a°,则∠BAD=
考点:三角形内角和定理,三角形的角平分线、中线和高,三角形的外角性质
专题:
分析:(1)先根据∠C=60°,求出∠DAC=30°求出∠BAC的度数,再根据角平分线的定义求出∠CAM的度数,由∠MAD=∠MAC-∠DAC即可得出结论.
(2)先根据∠C=60°,求出∠DAC=30°求出∠MAC的度数,再根据角平分线的定义求出∠BAM=∠CAM,由∠BAD=∠MAB+∠MAD即可得出结论.
(2)先根据∠C=60°,求出∠DAC=30°求出∠MAC的度数,再根据角平分线的定义求出∠BAM=∠CAM,由∠BAD=∠MAB+∠MAD即可得出结论.
解答:解:(1)∵AD⊥BC,∠C=60°,
∴∠DAC=30°,
∵∠BAD=50°,
∴∠BAC=50°+30°=80°,
∵AM是△ABC的角平分线,
∴∠MAC=
∠BAC=40°,
∴∠MAD=∠MAC-∠DAC=40°-30°=10°;
(2))∵AD⊥BC,∠C=60°,
∴∠DAC=30°,
∵∠MAD=a°,
∴∠MAC=30°+α°
∵AM是△ABC的角平分线,
∴∠MAB=∠MAC=
∠BAC,
∴∠BAD=∠MAB+∠MAD=30°+α°+α°=30°+2α°;
故答案为30°+2α°
∴∠DAC=30°,
∵∠BAD=50°,
∴∠BAC=50°+30°=80°,
∵AM是△ABC的角平分线,
∴∠MAC=
| 1 |
| 2 |
∴∠MAD=∠MAC-∠DAC=40°-30°=10°;
(2))∵AD⊥BC,∠C=60°,
∴∠DAC=30°,
∵∠MAD=a°,
∴∠MAC=30°+α°
∵AM是△ABC的角平分线,
∴∠MAB=∠MAC=
| 1 |
| 2 |
∴∠BAD=∠MAB+∠MAD=30°+α°+α°=30°+2α°;
故答案为30°+2α°
点评:本题考查的是三角形内角和定理、三角形的角平分线和高等知识,熟知三角形的内角和是180°是解答此题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
方程(x-1)2+(y-1)2=xy+7的所有正整数解有( )组.
| A、1 | B、2 | C、3 | D、4 |
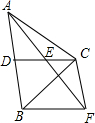 如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交于AE的延长线于F,连接BF.
如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交于AE的延长线于F,连接BF.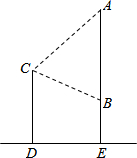 如图所示,小明站在地面上照镜子,镜子AB挂在和地面垂直的墙面AE上,镜子的高度AB为(1+
如图所示,小明站在地面上照镜子,镜子AB挂在和地面垂直的墙面AE上,镜子的高度AB为(1+ 如图,△ABC=90°,∠1=∠B.如果AC=8,BC=6,AB=10,求CD的长.
如图,△ABC=90°,∠1=∠B.如果AC=8,BC=6,AB=10,求CD的长.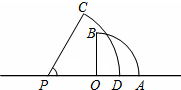 如图,以数轴上的原点O为圆心,6为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,10为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如果两个扇形的圆弧部分(
如图,以数轴上的原点O为圆心,6为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,10为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如果两个扇形的圆弧部分(
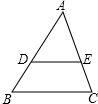 如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC=
如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC=