题目内容
8. 如图,在正方形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH,线段EG与FH是否存在特殊的位置关系或数量关系?证明你的结论.
如图,在正方形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH,线段EG与FH是否存在特殊的位置关系或数量关系?证明你的结论.
分析 根据正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,求出BE=CF=DG=AH,根据SAS推出△EBF≌△FCG≌△GDH≌△HAB,根据全等三角形的性质得出EF=FG=GH=HE,∠AEH=∠EFB,求出∠HEF=90°,根据正方形的判定得出四边形EFGH的形状是正方形即可.
解答  证明:连接HG,GF,EF,HE,
证明:连接HG,GF,EF,HE,
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=AD,
∵AE=BF=CG=DH,
∴BE=CF=DG=AH,
∴△EBF≌△FCG≌△GDH≌△HAB,
∴EF=FG=GH=HE,∠AEH=∠EFB,
∵∠B=90°,
∴∠EFB+∠FEB=90°,
∴∠AEH+∠FEB=90°,
∴∠HEF=90°,
∵EF=FG=GH=HE,
∴四边形EFGH的形状是正方形,
∴EG=HF,且EG⊥HF.
点评 本题考查了全等三角形的性质和判定,正方形的性质和判定的应用,解此题的关键是推出∠HEF=90°和EF=FG=GH=HE,题目比较典型,难度适中.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 如图,已知矩形ABCD,过D作BD的垂线,与BC延长线交于E点,F为BE的中点,连接DF,已知DF=4,设AB=x,AD=y,求代数式x2+(y-4)2的值.
如图,已知矩形ABCD,过D作BD的垂线,与BC延长线交于E点,F为BE的中点,连接DF,已知DF=4,设AB=x,AD=y,求代数式x2+(y-4)2的值.
 已知:如图,∠BCD=80°,CA平分∠BCD,∠1=40°,求∠B的大小.
已知:如图,∠BCD=80°,CA平分∠BCD,∠1=40°,求∠B的大小.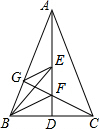 如图,在△ABC中,AD⊥BC于D,AB=AC,BE、BF将∠ABC三等分交AD于E、F,CF延长线交AB于G,求证:GE∥BF.
如图,在△ABC中,AD⊥BC于D,AB=AC,BE、BF将∠ABC三等分交AD于E、F,CF延长线交AB于G,求证:GE∥BF.
 如图,四边形ABCD是正方形,点F是BC的中点,FG⊥AF,点E在BC的延长线上,CG平分∠DCE,交FG于点G,AB=4,求CG.
如图,四边形ABCD是正方形,点F是BC的中点,FG⊥AF,点E在BC的延长线上,CG平分∠DCE,交FG于点G,AB=4,求CG.